题目内容

8．如果正多边形的一个内角是140°，则这个多边形是（　　）
A．正十边形B．正九边形C．正八边形D．正七边形

分析 首先根据一个正多边形的内角是140°，求出每个外角的度数是多少；然后根据外角和定理，求出这个正多边形的边数是多少即可．

解答 解：360°÷（180°-140°）
=360°÷40°
=9．
答：这个正多边形的边数是9．
故选：B．

点评 此题主要考查了多边形的内角与外角，要熟练掌握，解答此题的关键是要明确多边形的外角和定理．

练习册系列答案
相关题目
18．如图，点B是线段AC的黄金分割点（AB＞BC），则下列结论中正确的是（　　）
A．AC2=AB2+BC2B．BC2=AC•ABC．$\frac{AB}{AC}=\frac{\sqrt{5}-1}{2}$D．$\frac{BC}{AC}=\frac{\sqrt{5}-1}{2}$
19．计算：
（1）2+（-7）-（-13）
（2）19$\frac{1}{8}$+（-5$\frac{3}{4}$）+（-9$\frac{1}{8}$）-1.25
（3）（$\frac{1}{2}$-$\frac{3}{4}$+$\frac{1}{8}$）×（-24）
（4）18×（-$\frac{2}{3}$）+13×$\frac{2}{3}$-4×$\frac{2}{3}$
（5）1÷（-$\frac{2}{7}$）×$\frac{1}{7}$                       
（6）-32+1÷2×$\frac{1}{2}$-|-1|×（-0.5）2．
16．阅读下列内容：
$\frac{1}{1×2}$=1-$\frac{1}{2}$，
$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$，
$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$，
$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$，
…
$\frac{1}{n×（n+1）}$=$\frac{1}{n}$-$\frac{1}{n+1}$
请完成下面的问题：
（1）$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2014×2015}$=$\frac{2014}{2015}$；
（2）试求$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2013×2015}$的值．
3．将下列各数填入相应的集合中．
-7，0，$\frac{22}{7}$，-22$\frac{1}{3}$，-2.55555…，3.01，+9，4.020020002…，+10%，-2π．
无理数集合：{                     }；
负有理数集合：{                      }；
正分数集合：{                     }；
非负整数集合：{                    }．
13．如图，Rt△ABC中，∠ACB=90°，BC=6，AC=8，现将△ABC折叠，使点A与点B重合，折痕为DE，则tan∠CBE=$\frac{7}{24}$．
20．若直角三角形两直角边的比为5：12，斜边长为39，则此直角三角形的周长为90．
17．y=2x2-x-1的顶点坐标是（$\frac{1}{4}$，-$\frac{9}{8}$）．
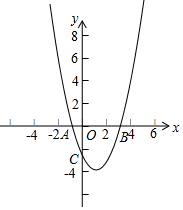18．在直角坐标平面中，O为坐标原点，二次函数y=x2+bx+c的图象与y轴的负半轴相交于点C（如图），点C的坐标为（0，-3），且BO=CO．
（1）求出B点坐标和这个二次函数的解析式；
（2）若顶点为D，求四边形ABDC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网