题目内容
18.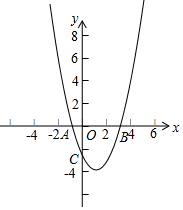 在直角坐标平面中,O为坐标原点,二次函数y=x2+bx+c的图象与y轴的负半轴相交于点C(如图),点C的坐标为(0,-3),且BO=CO.
在直角坐标平面中,O为坐标原点,二次函数y=x2+bx+c的图象与y轴的负半轴相交于点C(如图),点C的坐标为(0,-3),且BO=CO.(1)求出B点坐标和这个二次函数的解析式;
(2)若顶点为D,求四边形ABDC的面积.
分析 (1)由C的坐标得出CO的长,根据BO=CO得出BO的长,进而确定出B的坐标,将B和C的坐标代入二次函数解析式中求出b、c的值,即可确定出二次函数解析式;
(2)设抛物线的对称轴交x轴于E点,利用抛物线与x轴的交点问题求出A(-1,0),把解析式配成顶点式得到D(1,-4),然后根据三角形面积公式,利用S四边形ABDC=S△OAC+S梯形OCDE+S△EBD进行计算即可.
解答 解:(1)∵点C的坐标为(0,-3),且BO=CO,
∴点B的坐标为(3,0),
把(0,-3),(3,0)代入y=x2+bx+c,
得$\left\{\begin{array}{l}{c=-3}\\{9+3b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,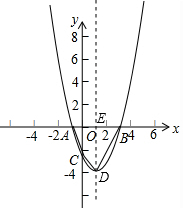 ∴y=x2-2x-3;
∴y=x2-2x-3;
(2)设抛物线的对称轴交x轴于E点,如图,
当y=0时,x2-2x-3=0,解得x1=-1,x2=3,则A(-1,0),
y=x2-2x-3=(x-1)2-4,
则D(1,-4),
S四边形ABDC=S△OAC+S梯形OCDE+S△EBD
=$\frac{1}{2}$×3×1+$\frac{1}{2}$(3+4)×1+$\frac{1}{2}$×2×4
=1.5+3.5+4
=9.
点评 此题考查了待定系数法求二次函数的解析式,二次函数的性质,熟练掌握待定系数法是解本题的关键.也考查了抛物线与x轴的交点问题和三角形面积公式.

练习册系列答案
相关题目
8.如果正多边形的一个内角是140°,则这个多边形是( )
| A. | 正十边形 | B. | 正九边形 | C. | 正八边形 | D. | 正七边形 |
7.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
下列说法:
①抛物线的开口向下;
②当x>-3时,y随x的增大而增大;
③二次函数的最小值是-2;
④抛物线的对称轴是x=-2.5,
其中正确的是④(填序号)
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
①抛物线的开口向下;
②当x>-3时,y随x的增大而增大;
③二次函数的最小值是-2;
④抛物线的对称轴是x=-2.5,
其中正确的是④(填序号)
 二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+a的图象不经过第四象限.
二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+a的图象不经过第四象限. 如图是由五块积木搭成,这几块积木都是相同的正方体,请分别画出这个图形的从正面看、从左面看、和从上面看的图形.
如图是由五块积木搭成,这几块积木都是相同的正方体,请分别画出这个图形的从正面看、从左面看、和从上面看的图形. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
 如图,已知线段AB=20米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
如图,已知线段AB=20米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )