题目内容
16.阅读下列内容:$\frac{1}{1×2}$=1-$\frac{1}{2}$,
$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,
$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,
$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$,
…
$\frac{1}{n×(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$
请完成下面的问题:
(1)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2014×2015}$=$\frac{2014}{2015}$;
(2)试求$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2013×2015}$的值.
分析 (1)根据给定分数间的关系,将其代入算式$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2014×2015}$中,消元后即可得出结论;
(2)根据给定的算式可找出$\frac{1}{1×3}$=$\frac{1}{2}$×(1-$\frac{1}{3}$),$\frac{1}{3×5}$=$\frac{1}{2}$×($\frac{1}{3}$-$\frac{1}{5}$),$\frac{1}{5×7}$=$\frac{1}{2}$×($\frac{1}{5}$-$\frac{1}{7}$),…,$\frac{1}{2013×2015}$=$\frac{1}{2}$×($\frac{1}{2013}$-$\frac{1}{2015}$),将其代入算式$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2013×2015}$中,消元后即可得出结论.
解答 解:(1)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2014×2015}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2014}$-$\frac{1}{2015}$=1-$\frac{1}{2015}$=$\frac{2014}{2015}$.
故答案为:$\frac{2014}{2015}$.
(2)∵$\frac{1}{1×3}$=$\frac{1}{2}$×(1-$\frac{1}{3}$),$\frac{1}{3×5}$=$\frac{1}{2}$×($\frac{1}{3}$-$\frac{1}{5}$),$\frac{1}{5×7}$=$\frac{1}{2}$×($\frac{1}{5}$-$\frac{1}{7}$),…,$\frac{1}{2013×2015}$=$\frac{1}{2}$×($\frac{1}{2013}$-$\frac{1}{2015}$),
∴$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2013×2015}$=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{2013}$-$\frac{1}{2015}$)=$\frac{1}{2}$×$\frac{2014}{2015}$=$\frac{1007}{2015}$.
点评 本题考查了规律型中的数字的变化类,根据给定材料找出$\frac{1}{1×3}$=$\frac{1}{2}$×(1-$\frac{1}{3}$),$\frac{1}{3×5}$=$\frac{1}{2}$×($\frac{1}{3}$-$\frac{1}{5}$),$\frac{1}{5×7}$=$\frac{1}{2}$×($\frac{1}{5}$-$\frac{1}{7}$),…,$\frac{1}{2013×2015}$=$\frac{1}{2}$×($\frac{1}{2013}$-$\frac{1}{2015}$)是解题的关键.

| A. | 正十边形 | B. | 正九边形 | C. | 正八边形 | D. | 正七边形 |
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论错误的是( )| A. | a<0 | B. | 当-1<x<3时,y<0 | C. | b2-4ac>0 | D. | $-\frac{b}{2a}=1$ |
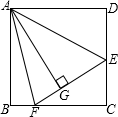 如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则:
如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则: 如图是由五块积木搭成,这几块积木都是相同的正方体,请分别画出这个图形的从正面看、从左面看、和从上面看的图形.
如图是由五块积木搭成,这几块积木都是相同的正方体,请分别画出这个图形的从正面看、从左面看、和从上面看的图形.