题目内容
20．若直角三角形两直角边的比为5：12，斜边长为39，则此直角三角形的周长为90．分析 设直角三角形的两直角边分别为5x，12x，再根据勾股定理求出x的值，进而可得出结论．
解答 解：∵直角三角形两直角边的比为5：12，斜边长为39，
∴设直角三角形的两直角边分别为5x，12x，
∵（5x）2+（12x）2=392，解得x=3，
∴5x=15，12x=36，
∴此直角三角形的周长=15+36+39=90．
故答案为：90．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
10．
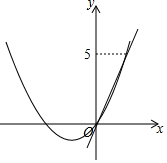如图，抛物线y=$\frac{1}{2}$x2+$\frac{3}{2}$x与直线y=kx的交点A的纵坐标是5，则不等式$\frac{1}{2}$x2+$\frac{3}{2}$x-kx＞0的解集是（ ）
如图，抛物线y=$\frac{1}{2}$x2+$\frac{3}{2}$x与直线y=kx的交点A的纵坐标是5，则不等式$\frac{1}{2}$x2+$\frac{3}{2}$x-kx＞0的解集是（ ）| A． | x＞0 | B． | -2＜x＜0 | C． | -5＜x＜2 | D． | x＜0或x＞2 |
8．如果正多边形的一个内角是140°，则这个多边形是（ ）
| A． | 正十边形 | B． | 正九边形 | C． | 正八边形 | D． | 正七边形 |
将以长方形纸片如图折叠，若∠1=140°，则∠2=110°．
5．
二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论错误的是（ ）
二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论错误的是（ ）| A． | a＜0 | B． | 当-1＜x＜3时，y＜0 | C． | b2-4ac＞0 | D． | $-\frac{b}{2a}=1$ |
二次函数y=ax2+bx+c的图象如图，则一次函数y=bx+a的图象不经过第四象限．