题目内容
18. 如图,点B是线段AC的黄金分割点(AB>BC),则下列结论中正确的是( )
如图,点B是线段AC的黄金分割点(AB>BC),则下列结论中正确的是( )| A. | AC2=AB2+BC2 | B. | BC2=AC•AB | C. | $\frac{AB}{AC}=\frac{\sqrt{5}-1}{2}$ | D. | $\frac{BC}{AC}=\frac{\sqrt{5}-1}{2}$ |
分析 根据黄金分割点的定义,知AC为较长线段;则AB=$\frac{\sqrt{5}-1}{2}$AC,进而判断即可.
解答 解:因为点B是线段AC的黄金分割点(AB>BC),
所以AB=$\frac{\sqrt{5}-1}{2}$AC,
故选C
点评 本题主要考查了黄金分割的定义:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.

练习册系列答案
相关题目
3.下列各对数:-2与+(-2),+(+3)与-3,-(-$\frac{1}{2}$)与+(-$\frac{1}{2}$),-(-12)与+(+12),-(+1)与-(-1).其中互为相反数的有( )
| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |
10.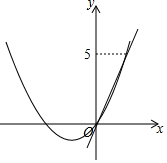 如图,抛物线y=$\frac{1}{2}$x2+$\frac{3}{2}$x与直线y=kx的交点A的纵坐标是5,则不等式$\frac{1}{2}$x2+$\frac{3}{2}$x-kx>0的解集是( )
如图,抛物线y=$\frac{1}{2}$x2+$\frac{3}{2}$x与直线y=kx的交点A的纵坐标是5,则不等式$\frac{1}{2}$x2+$\frac{3}{2}$x-kx>0的解集是( )
 如图,抛物线y=$\frac{1}{2}$x2+$\frac{3}{2}$x与直线y=kx的交点A的纵坐标是5,则不等式$\frac{1}{2}$x2+$\frac{3}{2}$x-kx>0的解集是( )
如图,抛物线y=$\frac{1}{2}$x2+$\frac{3}{2}$x与直线y=kx的交点A的纵坐标是5,则不等式$\frac{1}{2}$x2+$\frac{3}{2}$x-kx>0的解集是( )| A. | x>0 | B. | -2<x<0 | C. | -5<x<2 | D. | x<0或x>2 |
8.如果正多边形的一个内角是140°,则这个多边形是( )
| A. | 正十边形 | B. | 正九边形 | C. | 正八边形 | D. | 正七边形 |
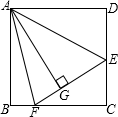 如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则:
如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则: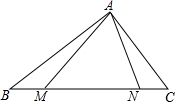 如图所示,在△ABC中,∠BAC=∠ACB,M,N分别是边BC上两点,∠BAM=∠CAN,并且∠AMN=∠MAN,求∠MAC.
如图所示,在△ABC中,∠BAC=∠ACB,M,N分别是边BC上两点,∠BAM=∠CAN,并且∠AMN=∠MAN,求∠MAC.