题目内容
16.计算(1)(-$\frac{2}{3}$xy)•($\frac{2}{3}$x2y-4xy2+$\frac{4}{3}$y)
(2)(-x2)3•x2+(2x2)4-3(-x)3•x5
(3)2-2×(π-3)0-(-3-1)2×32.
分析 (1)根据单项式与多项式相乘的法则计算出各数即可;
(2)先根据幂的乘方与积的乘方法则分别计算出各数,再算乘法,加减即可;
(3)分别根据0指数幂及负整数指数幂的计算法则计算出各数,再算乘法,最后算加减即可.
解答 解:(1)原式=-$\frac{4}{9}$x3y2+$\frac{8}{3}$x2y3-$\frac{8}{9}$xy2;
(2)原式=(-x6)•x2+16x8+3x8
=-x8+16x8+3x8
=-18x8;
(3)原式=$\frac{1}{4}$×1-$\frac{1}{9}$×9
=$\frac{1}{4}$-1
=-$\frac{3}{4}$.
点评 本题考查的是整式的混合运算,“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.

练习册系列答案
相关题目
1. 如图,矩形ABCD的面积为16cm2,对交线交于点O;以AB、AO为邻边作平行四边AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B,…;依此类推,则平行四边形AO4C5B的面积为( )
如图,矩形ABCD的面积为16cm2,对交线交于点O;以AB、AO为邻边作平行四边AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B,…;依此类推,则平行四边形AO4C5B的面积为( )
 如图,矩形ABCD的面积为16cm2,对交线交于点O;以AB、AO为邻边作平行四边AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B,…;依此类推,则平行四边形AO4C5B的面积为( )
如图,矩形ABCD的面积为16cm2,对交线交于点O;以AB、AO为邻边作平行四边AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B,…;依此类推,则平行四边形AO4C5B的面积为( )| A. | $\frac{1}{2}$cm2 | B. | 1cm2 | C. | 2cm2 | D. | 4cm2 |
5.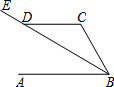 如图,直线AB∥CD,BE平分∠ABC,交CD于点D,∠CDB=30°,那么∠C的度数为( )
如图,直线AB∥CD,BE平分∠ABC,交CD于点D,∠CDB=30°,那么∠C的度数为( )
 如图,直线AB∥CD,BE平分∠ABC,交CD于点D,∠CDB=30°,那么∠C的度数为( )
如图,直线AB∥CD,BE平分∠ABC,交CD于点D,∠CDB=30°,那么∠C的度数为( )| A. | 150° | B. | 130° | C. | 120° | D. | 100° |
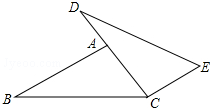 如图,点D、A、C在同一直线上,AB∥CE,AB=CD,∠B=∠D,求证:BC=DE.
如图,点D、A、C在同一直线上,AB∥CE,AB=CD,∠B=∠D,求证:BC=DE.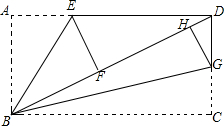 如图,在矩形ABCD中,AB=6,BC=8,E,G分别在AD,CD上,沿BE,BG折叠矩形,点A和点C分别落在BD上的点F,H处.
如图,在矩形ABCD中,AB=6,BC=8,E,G分别在AD,CD上,沿BE,BG折叠矩形,点A和点C分别落在BD上的点F,H处.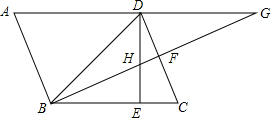 如图,BD是平行四边形ABCD的对角线,若∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE与BF相交于H,BF与AD的延长线相交于G.求证:
如图,BD是平行四边形ABCD的对角线,若∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE与BF相交于H,BF与AD的延长线相交于G.求证: 如图,已知在等腰△ABC中,∠A=∠B=30°.
如图,已知在等腰△ABC中,∠A=∠B=30°.