题目内容
6．
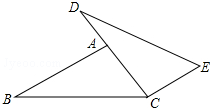如图，点D、A、C在同一直线上，AB∥CE，AB=CD，∠B=∠D，求证：BC=DE．
分析 根据由两个角和其中一角的对边相等的两个三角形全等证明△ABC≌△CDE，由全等三角形的性质即可得到BC=DE．
解答 证明：∵AB∥EC，
∴∠BAC=∠DCE，
在△ABC和△CDE中，
$\left\{\begin{array}{l}{∠BAC=∠DCE}\\{∠B=∠D}\\{AB=CD}\end{array}\right.$，
∴△ABC≌△CDE，
∴BC=DE．
点评 本题考查了全等三角形的判定和性质，全等三角形角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
如图所示，在?ABCD中，BF⊥AD于F，BE⊥CD于E，若∠A=60°，AF=3cm，CE=2cm，则?ABCD的周长为20cm．．
如图，点O，A在数轴上表示的数分别是0，0.1．将线段OA分成100等份，其分点由左向右依次为M1，M2，…，M99；再将线段OM1，分成100等份，其分点由左向右依次为N1，N2，…，N99；继续将线段ON1分成100等份，其分点由左向右依次为P1，P2．…，P99．则点P26所表示的数用科学记数法表示为2.6×10-6．