题目内容
1. 如图,矩形ABCD的面积为16cm2,对交线交于点O;以AB、AO为邻边作平行四边AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B,…;依此类推,则平行四边形AO4C5B的面积为( )
如图,矩形ABCD的面积为16cm2,对交线交于点O;以AB、AO为邻边作平行四边AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B,…;依此类推,则平行四边形AO4C5B的面积为( )| A. | $\frac{1}{2}$cm2 | B. | 1cm2 | C. | 2cm2 | D. | 4cm2 |
分析 根据平行四边形的性质得出O1A=O1C1,O1B=O1O,求出SAO1B=$\frac{1}{2}$S△ABC1=$\frac{1}{4}$S?ABCD=4cm2,求出四边形ABC1O是菱形,推出AC1=2O1A,O1B=2O1O2=2O2B,AC1⊥BO1,平行四边形ABC1O的面积是AC1×BO1=8cm2,推出△ABO2的面积是2cm2,同理平行四边形ABC2O2的面积是4cm2,平行四边形ABC3O3的面积是2cm2,平行四边形ABC4O4的面积是1cm2,平行四边形AO4C5B的面积是$\frac{1}{2}$cm2.
解答 解:∵四边形ABCD是平行四边形,
∴O1A=O1C1,O1B=O1O,
∴SAO1B=$\frac{1}{2}$S△ABC1=$\frac{1}{4}$S?ABCD=4cm2,
∵四边形ABC1O1是平行四边形,O1A=O1B,
∴四边形ABC1O是菱形,
∴AC1=2O2A,O1B=2O1O2=2O2B,AC1⊥BO1,
∴平行四边形ABC1O1的面积是AC1×BO1=×2AO2×BO1=2×AO2×BO1=2×4cm2=8cm2,
∴△ABO2的面积=2cm2,
同理平行四边形ABC2O2的面积是4cm2,
平行四边形ABC3O3的面积是2cm2,
平行四边形ABC4O4的面积是1cm2,
平行四边形AO4C5B的面积是$\frac{1}{2}$cm2,
故选:A.
点评 本题考查了平行四边形性质,菱形的性质和判定,三角形的面积等知识点,此题的关键是能根据求出的结果得出规律,注意:等底等高的三角形的面积相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.以下列各组数据为边长,可以构成等腰三角形的是( )
| A. | 2,3,4 | B. | 5,5,10 | C. | 2,2,1 | D. | 1,2,3 |
13.某中学八年级同学在综合实践学习课上,做大蒜在相同条件下的发芽实验,结果统计如表,则试验中大蒜发芽的概率估计是0.95(精确到0.01).
| 种子粒数 | 100 | 500 | 1000 | 2000 | 3000 |
| 发芽粒数 | 96 | 470 | 948 | 1912 | 2853 |
| 发芽频率 | 0.96 | 0.94 | 0.948 | 0.956 | 0.951 |
 如图,点O,A在数轴上表示的数分别是0,0.1.将线段OA分成100等份,其分点由左向右依次为M1,M2,…,M99;再将线段OM1,分成100等份,其分点由左向右依次为N1,N2,…,N99;继续将线段ON1分成100等份,其分点由左向右依次为P1,P2.…,P99.则点P26所表示的数用科学记数法表示为2.6×10-6.
如图,点O,A在数轴上表示的数分别是0,0.1.将线段OA分成100等份,其分点由左向右依次为M1,M2,…,M99;再将线段OM1,分成100等份,其分点由左向右依次为N1,N2,…,N99;继续将线段ON1分成100等份,其分点由左向右依次为P1,P2.…,P99.则点P26所表示的数用科学记数法表示为2.6×10-6. 如图,在△ABC中,∠B=45°,∠C=75°,AC=2$\sqrt{6}$,AC的中点为D,若长度为3的线段PQ(P在Q的左侧)在直线BC上滑动,则AP+DQ的最小值为$\frac{3\sqrt{10}+\sqrt{30}}{2}$..
如图,在△ABC中,∠B=45°,∠C=75°,AC=2$\sqrt{6}$,AC的中点为D,若长度为3的线段PQ(P在Q的左侧)在直线BC上滑动,则AP+DQ的最小值为$\frac{3\sqrt{10}+\sqrt{30}}{2}$..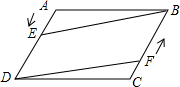 如图,在?ABCD中,点E从A向D运动,点F从C向B运动,点E的运动速度m与点F的运动速度n满足m=n关系时,四边形BEDF为平行四边形.
如图,在?ABCD中,点E从A向D运动,点F从C向B运动,点E的运动速度m与点F的运动速度n满足m=n关系时,四边形BEDF为平行四边形.