题目内容
9.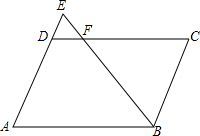 ?ABCD的面积是30cm,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大8cm,且AD=5cm,那么DE=2cm.
?ABCD的面积是30cm,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大8cm,且AD=5cm,那么DE=2cm.
分析 如果△FBC的面积比△FDE的面积大9平方厘米,那么平行四边形ABCD的面积比△ABE就大9平方厘米,三角形ABE的面积是30-9=21平方厘米,平行四边形ABCD的底边AD上的高是30÷5=6cm,则三角形ABE底边AE上的高就是6厘米,根据三角形的面积公式可得:底AE=21×2÷6,然后减去5cm,就是DE的值.
解答 解:∵平行四边形ABCD的面积是30cm2,△FBC的面积比△FDE的面积大9cm2,
∴30-9=21cm2,
30÷5=6cm,
故21×2÷6-5
=7-5
=2cm.
答:DE等于2cm.
故答案为:2.
点评 此题主要考查了平行四边形性质,利用已知得出平行四边形ABCD的面积比△ABE大9平方米是解题关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
18.已知n是一个正整数,若$\sqrt{135n}$与$\sqrt{3}$能合并,则n的最小值是( )
| A. | 3 | B. | 5 | C. | 15 | D. | 25 |
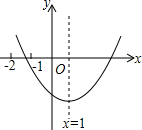 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc>0;③9a+3b+c<0.其中,正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc>0;③9a+3b+c<0.其中,正确结论的个数是( )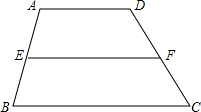 如图,在四边形ABCD中,AD∥BC,E、F分别是AB、CD两边的中点,求证:EF∥AD∥BC,EF=$\frac{1}{2}$(AD+BC)
如图,在四边形ABCD中,AD∥BC,E、F分别是AB、CD两边的中点,求证:EF∥AD∥BC,EF=$\frac{1}{2}$(AD+BC)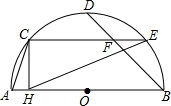 如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、