题目内容
4.化简($\frac{{2x}^{2}+2x}{{x}^{2}-1}-\frac{{x}^{2}-x}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$,再判断该代数式的值能否等于-17,并说明理由.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,令其值为-17,即可做出判断.
解答 解:原式=[$\frac{2x(x+1)}{(x+1)(x-1)}$-$\frac{x(x-1)}{(x-1)^{2}}$]•$\frac{x+1}{x}$=$\frac{2(x+1)}{x-1}$-$\frac{x+1}{x-1}$=$\frac{2x+2-x-1}{x-1}$=$\frac{x+1}{x-1}$,
若代数式的值为-17,则有$\frac{x+1}{x-1}$=-17,即x+1=-17x+17,
解得:x=$\frac{8}{9}$,
经检验x=$\frac{8}{9}$满足题意,
则该代数式的值能等于-17.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目

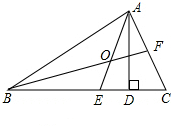 已知:如图,△ABC中,AD、AE分别是△ABC的高和角平分线,BF是∠ABC的平分线,BF与AE交于O,若∠ABC=40°,∠C=60°,求∠DAE、∠BOE的度数.
已知:如图,△ABC中,AD、AE分别是△ABC的高和角平分线,BF是∠ABC的平分线,BF与AE交于O,若∠ABC=40°,∠C=60°,求∠DAE、∠BOE的度数.
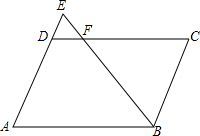 ?ABCD的面积是30cm,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大8cm,且AD=5cm,那么DE=2cm.
?ABCD的面积是30cm,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大8cm,且AD=5cm,那么DE=2cm.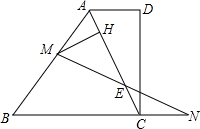 如图,直角梯形ABCD中,AD∥BC,CD=2,AB=BC,AD=1,动点M、N分别在AB边和BC的延长线运动,而且AM=CN,联结AC交MN于E,MH⊥AC于H,则EH=$\frac{\sqrt{5}}{2}$.
如图,直角梯形ABCD中,AD∥BC,CD=2,AB=BC,AD=1,动点M、N分别在AB边和BC的延长线运动,而且AM=CN,联结AC交MN于E,MH⊥AC于H,则EH=$\frac{\sqrt{5}}{2}$.