题目内容
20.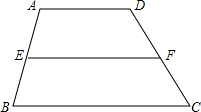 如图,在四边形ABCD中,AD∥BC,E、F分别是AB、CD两边的中点,求证:EF∥AD∥BC,EF=$\frac{1}{2}$(AD+BC)
如图,在四边形ABCD中,AD∥BC,E、F分别是AB、CD两边的中点,求证:EF∥AD∥BC,EF=$\frac{1}{2}$(AD+BC)
分析 连接AF并延长,交BC延长线于点M,根据ASA证明△ADF≌△MCF,判断EF是△ABM的中位线,根据三角形中位线定理即可得出结论.
解答 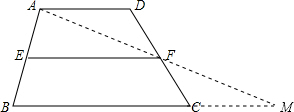 证明:连接AF并延长,交BC延长线于点M,
证明:连接AF并延长,交BC延长线于点M,
∵AD∥BC,
∴∠D=∠FCM,
∵F是CD中点,
∴DF=CF,
在△ADF和△MCF中,
$\left\{\begin{array}{l}{∠D=∠FCM}\\{DF=CF}\\{∠AFD=∠MFC}\end{array}\right.$,
∴△ADF≌△MCF(ASA),
∴AF=FM,AD=CM,
∴EF是△ABM的中位线,
∴EF∥BC∥AD,EF=$\frac{1}{2}$BM=$\frac{1}{2}$(AD+BC).
点评 本题实际上考查了梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半.其中利用了全等三角形的判定与性质,三角形中位线定理,准确作出辅助线是解题关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
10.对于代数式3x3y-2x2y2+5xy3-1,下列说法不正确的是( )
| A. | 它按y的升幂排列 | B. | 它按x的降幂排列 | C. | 它的常数项是-1 | D. | 它是四次四项式 |
11.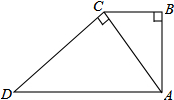 如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=3,DC=5,则△ABC与△DCA的面积比为( )
如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=3,DC=5,则△ABC与△DCA的面积比为( )
 如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=3,DC=5,则△ABC与△DCA的面积比为( )
如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=3,DC=5,则△ABC与△DCA的面积比为( )| A. | 2:3 | B. | 3:5 | C. | 9:25 | D. | $\sqrt{3}$:$\sqrt{5}$ |
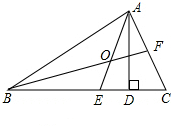 已知:如图,△ABC中,AD、AE分别是△ABC的高和角平分线,BF是∠ABC的平分线,BF与AE交于O,若∠ABC=40°,∠C=60°,求∠DAE、∠BOE的度数.
已知:如图,△ABC中,AD、AE分别是△ABC的高和角平分线,BF是∠ABC的平分线,BF与AE交于O,若∠ABC=40°,∠C=60°,求∠DAE、∠BOE的度数.
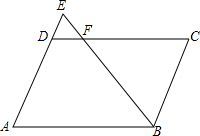 ?ABCD的面积是30cm,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大8cm,且AD=5cm,那么DE=2cm.
?ABCD的面积是30cm,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大8cm,且AD=5cm,那么DE=2cm.