题目内容
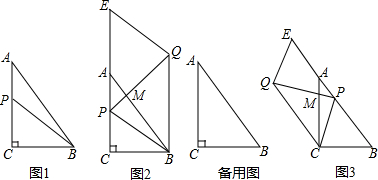
16. 如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、EC相交于F点,连接AC、EH,下列结论:
①CE=2CH;②∠ACH=∠CEH;③∠CFD=2∠ACH,
其中正确的结论是( )
| A. | ①②③ | B. | 只有①② | C. | 只有①③ | D. | 只有③ |
分析 连结OC、BC、OD,OD交CE于G,如图,由于C、D、E是半圆的四等分点,根据垂径定理得到OD⊥CE,CE=2CG,根据圆心角、弧、弦的关系得到∠AOC=∠COD=45°,根据圆周角定理得∠BCE=∠ABC,再证明四边形CHOG为正方形,则CH=CG,所以CE=2CH;利用等角的余角相等得∠ACH=∠ABC,而∠CEH所对的弧大于AC弧,则∠CEH>∠ABC,所以∠ACH<∠CEH;利用CE∥AB得到∠CFD=∠ABD,而∠ABD=2∠ABC=2∠ACH,于是有∠CFD=2∠ACH.
解答 解: 连结OC、BC、OD,OD交CE于G,如图,
连结OC、BC、OD,OD交CE于G,如图,
∵C、D、E是半圆的四等分点,
∴OD⊥CE,∠AOC=∠COD=45°,∠BCE=∠ABC,
∴CE=2CG,CE∥AB
∵CH⊥AB,
∴四边形CHOG为正方形,
∴CH=CG,
∴CE=2CH,所以①正确;
∵AB为直径,
∴∠ACB=90°,
∴∠ACH=∠ABC,
而∠CEH所对的弧大于AC弧,
∴∠CEH>∠ABC,
∴∠ACH<∠CEH,所以②错误;
∵CE∥AB,
∴∠CFD=∠ABD,
∵弧AC=弧CD,
∴∠ACB=∠CBD,
∴∠ABD=2∠ABC=2∠ACH,
∴∠CFD=2∠ACH,所以③正确.
故选C.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了圆心角、弧、弦的关系.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
8.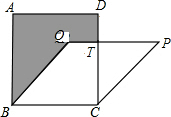 如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )
如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )
 如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )
如图所示,正方形ABCD的面积为169cm2,菱形BCPQ的面积为156cm2.则阴影部分的面积是( )| A. | 23cm2 | B. | 33cm2 | C. | 43cm2 | D. | 53cm2 |
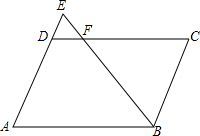 ?ABCD的面积是30cm,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大8cm,且AD=5cm,那么DE=2cm.
?ABCD的面积是30cm,E为AD边延长线上的一点,EB与DC交于F点,如果△FBC的面积比△FDE的面积大8cm,且AD=5cm,那么DE=2cm.
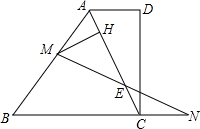 如图,直角梯形ABCD中,AD∥BC,CD=2,AB=BC,AD=1,动点M、N分别在AB边和BC的延长线运动,而且AM=CN,联结AC交MN于E,MH⊥AC于H,则EH=$\frac{\sqrt{5}}{2}$.
如图,直角梯形ABCD中,AD∥BC,CD=2,AB=BC,AD=1,动点M、N分别在AB边和BC的延长线运动,而且AM=CN,联结AC交MN于E,MH⊥AC于H,则EH=$\frac{\sqrt{5}}{2}$.