题目内容
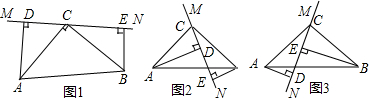
5.如图,在△ABC中,∠ACB=90°,AC=BC,直线MN过点C,且AD⊥MN于点D,BE⊥MN于点E,在MN绕点C旋转过程中,以上关系保持不变(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2位置时,DE、AD、BE三者之间有怎样的等量关系,证明你的结论;
(3)当直线MN绕点C旋转到图3位置时,试问:DE、AD、BE三者之间又有怎样的等量关系?请直接写出结论.
分析 (1)由∠ACB=90°,得∠ACD+∠BCE=90°,而AD⊥MN于D,BE⊥MN于E,则∠ADC=∠CEB=90°,根据等角的余角相等得到∠ACD=∠CBE,易得Rt△ADC≌Rt△CEB,所以AD=CE,DC=BE,即可得到DE=DC+CE=BE+AD.
(2)根据等角的余角相等得到∠ACD=∠CBE,易得△ADC≌△CEB,得到AD=CE,DC=BE,所以DE=CE-CD=AD-BE;
(3)DE、AD、BE具有的等量关系为:DE=BE-AD.证明的方法与(2)相同.
解答 (1)证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
而AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE.
在△ADC和△CEB中,
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠ACD=∠CBE}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=DC+CE=BE+AD;
(2)DE=CE-CD=AD-BE.
理由如下:
在△ADC和△CEB中,
$\left\{\begin{array}{l}{∠ADC=∠CEB=90°}\\{∠ACD=∠CBE}\\{AC=CB}\end{array}\right.$,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=CE-CD=AD-BE;
(3)DE=BE-AD.
易证得△ADC≌△CEB,
∴AD=CE,DC=BE,
∴DE=CD-CE=BE-AD.
点评 本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角.也考查了直角三角形全等的判定与性质.

| 3 | 4 | x |
| -2 | y | a |
| 2y-x | c | b |
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
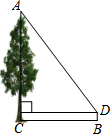 如图,B为地面上一点,测得点B到树底部C的距离为10米,在点B处放置一个1米高的测角仪BD,并测得树顶A的仰角为53°,则树高AC约为14.3 米(精确到0.1米).
如图,B为地面上一点,测得点B到树底部C的距离为10米,在点B处放置一个1米高的测角仪BD,并测得树顶A的仰角为53°,则树高AC约为14.3 米(精确到0.1米).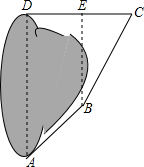 某实践小组去公园测量人工湖AD的长度.小明进行如下测量:点D在点A的正北方向,点B在点A的北偏东50°方向,AB=40米.点E在点B的正北方向,点C在点B的北偏东30°方向,CE=30米.点C和点E都在点D的正东方向,求AD的长(结果精确到1米).(参考数据:$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
某实践小组去公园测量人工湖AD的长度.小明进行如下测量:点D在点A的正北方向,点B在点A的北偏东50°方向,AB=40米.点E在点B的正北方向,点C在点B的北偏东30°方向,CE=30米.点C和点E都在点D的正东方向,求AD的长(结果精确到1米).(参考数据:$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)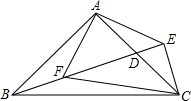 已知如图,Rt△ABC中,∠BAC=90°,AB=AC,D是AC的中点,过C作CE⊥BD交BD的延长线于E,连结AE,过A作AF⊥AE交BD于F.
已知如图,Rt△ABC中,∠BAC=90°,AB=AC,D是AC的中点,过C作CE⊥BD交BD的延长线于E,连结AE,过A作AF⊥AE交BD于F.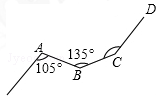 如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角∠A是105度,第二次拐的角∠B是135度,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C=150°.
如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角∠A是105度,第二次拐的角∠B是135度,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C=150°.