题目内容
10.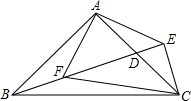 已知如图,Rt△ABC中,∠BAC=90°,AB=AC,D是AC的中点,过C作CE⊥BD交BD的延长线于E,连结AE,过A作AF⊥AE交BD于F.
已知如图,Rt△ABC中,∠BAC=90°,AB=AC,D是AC的中点,过C作CE⊥BD交BD的延长线于E,连结AE,过A作AF⊥AE交BD于F.(1)求证:△AEF是等腰直角三角形;
(2)连结CF,求证:CF=AC.
分析 (1)先证明∠BAF=∠CAE,再证∠ABF=∠ACE,由ASA证明△ABF≌△ACE,得出AE=AF,即可得出结论;
(2)过点A作AM⊥BD于点M,先证明△AMD≌△CED,得出AM=CE,再证明BM=EF,然后证明△CEF≌△AMB,得出CF=AB,即可得出结论.
解答 (1)证明:∵AE⊥AF,
∴∠EAF=90°,
∵∠BAC=90°,
∴∠BAF=∠CAE,
∵BE⊥CE,
∴∠BEC=90°,
∵∠ADB=∠CDE,
∴∠ABF=∠ACE,
在△ABF和△ACE中,
$\left\{\begin{array}{l}{∠BAF=∠CAE}&{\;}\\{AB=AC}&{\;}\\{∠ABF=∠ACE}&{\;}\end{array}\right.$,
∴△ABF≌△ACE(ASA),
∴AE=AF,
∴△AEF是等腰直角三角形;
(2)证明:过点A作AM⊥BD于点M,如图所示: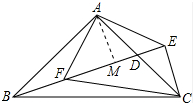
则∠AME=90°,
∵BE⊥CE,
∴∠BEC=90°,
∵D为AC中点,
∴AD=CD
在△AMD和△CED中,
$\left\{\begin{array}{l}{∠ADM=∠CDE}&{\;}\\{∠AMD=∠CED=90°}&{\;}\\{AD=CD}&{\;}\end{array}\right.$,
∴△AMD≌△CED(AAS),
∴AM=CE,
∵△AEF为等腰直角三角形,AM⊥BD,
∴AM=MF=ME,
∴AM=MF=ME=CE,EF=2AM,
由(1)知:△ABF≌△ACE,
∴BF=EC,
∴BM=2AM,
∴BM=EF,
在△CEF和△AMB中,
$\left\{\begin{array}{l}{CE=AM}&{\;}\\{∠CEB=∠AMD}&{\;}\\{EF=BM}&{\;}\end{array}\right.$,
∴△CEF≌△AMB(SAS)
∴CF=AB,
∴CF=AC.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握全等三角形的判定方法,证明三角形全等是解决问题的关键.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案 如图,如果数轴上A,B两点表示的数互为相反数,那么点B表示的数为( )
如图,如果数轴上A,B两点表示的数互为相反数,那么点B表示的数为( )| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
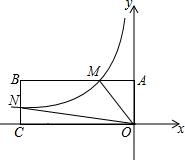 如图,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合,OC在x轴的负半轴上,OA在y轴的正半轴上,顶点B的坐标为(-6,1).反比例函数y=-$\frac{2}{x}$(x<0)的图象与AB交于点M,与BC交于点N,若点P在y轴上,使S△OMP=S四边形OMBN,则点P的坐标为(0,4)或(0,-4).
如图,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合,OC在x轴的负半轴上,OA在y轴的正半轴上,顶点B的坐标为(-6,1).反比例函数y=-$\frac{2}{x}$(x<0)的图象与AB交于点M,与BC交于点N,若点P在y轴上,使S△OMP=S四边形OMBN,则点P的坐标为(0,4)或(0,-4).
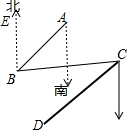 如图,B处在A处南偏西45°的方向,C处在B处的北偏东80°,若D处在C处的南偏西45°的方向,试说明:CD∥AB.
如图,B处在A处南偏西45°的方向,C处在B处的北偏东80°,若D处在C处的南偏西45°的方向,试说明:CD∥AB.