题目内容
1.列方程或方程组解应用题:小明坚持长跑健身.他从家匀速跑步到学校,通常需30分钟.某周日,小明与同学相约早上八点学校见,他七点半从家跑步出发,平均每分钟比平时快了40米,结果七点五十五分就到达了学校,求小明家到学校的距离.
分析 设小明家到学校的距离为x米,根据“小明与同学相约早上八点学校见,他七点半从家跑步出发,平均每分钟比平时快了40米,结果七点五十五分就到达了学校”建立方程,解方程即可.
解答 解:设小明家到学校的距离为x米,
由题意,得$\frac{x}{30}$+40=$\frac{x}{25}$,
解得x=6000.
答:小明家到学校的距离为6000米.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
11.若不等式组$\left\{\begin{array}{l}{1+x<a}\\{3-x≤0}\end{array}\right.$有解,则实数a的取值范围是( )
| A. | a<4 | B. | a≤4 | C. | a>4 | D. | a≥4 |
12.某射击教练对甲、乙两个射击选手的5次成绩(单位:环)进行了统计,如表
所示:设甲、乙两人射击成绩的平均数分别为$\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,射击成绩的方差分别为${s_甲}^2$、${s_乙}^2$,则下列判断中正确的是( )
| 甲 | 10 | 9 | 8 | 5 | 8 |
| 乙 | 8 | 8 | 7 | 9 | 8 |
| A. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,${s_甲}^2$>${s_乙}^2$ | B. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2$<${s_乙}^2$ | ||
| C. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2={s_乙}^2$ | D. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2$>${s_乙}^2$ |
6. 如图,如果数轴上A,B两点表示的数互为相反数,那么点B表示的数为( )
如图,如果数轴上A,B两点表示的数互为相反数,那么点B表示的数为( )
 如图,如果数轴上A,B两点表示的数互为相反数,那么点B表示的数为( )
如图,如果数轴上A,B两点表示的数互为相反数,那么点B表示的数为( )| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
13.为了倡导绿色出行,某市为市民提供了自行车租赁服务,其收费标准如下:
如果小明某次租赁自行车3小时,缴费14元,请判断小明该次租赁自行车所在地区的类别是B类(填“A、B、C”中的一个).
| 地区类别 | 首小时内 | 首小时外 | 备注 |
| A类 | 1.5元/15分钟 | 2.75元/15分钟 | 不足15分钟时 按15分钟收费 |
| B类 | 1.0元/15分钟 | 1.25元/15分钟 | |
| C类 | 免费 | 0.75元/15分钟 |
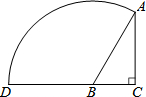 如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,以B为圆心,BA为半径画弧交CB的延长线于点D,则$\widehat{AD}$的长为$\frac{4π}{3}$.
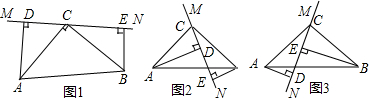
如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,以B为圆心,BA为半径画弧交CB的延长线于点D,则$\widehat{AD}$的长为$\frac{4π}{3}$.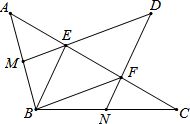 如图,在△ABC中,M,N分别是边AB、BC的中点,E、F是边AC上的三等分点,连接ME、NF且延长后交于点D,连接BE、BF
如图,在△ABC中,M,N分别是边AB、BC的中点,E、F是边AC上的三等分点,连接ME、NF且延长后交于点D,连接BE、BF