题目内容
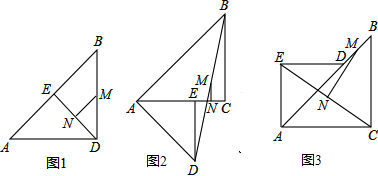
3.已知等腰Rt△ABC和等腰Rt△AED中,∠ACB=∠AED=90°,且AD=AC.(1)发现:如图1,当点E在AB上且点C和点D重合时,若点M、N分别是DB、EC的中点,则MN与EC的位置关系是MN⊥EC,MN与EC的数量关系是MN=$\frac{1}{2}EC$.
(2)探究:若把(1)小题中的△AED绕点A顺时针旋转45°得到的图2,连接BD和EC,并连接DB、EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,请给予证明,若不成立,请说明理由.
(3)若把(1)小题中的△AED绕点A逆时针旋转45°得到的图3,连接BD和EC,并连接DB、EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,请给予证明,若不成立,请说明理由.
分析 (1)根据中位线定理,结合等腰直角三角形性质即可直接得出结论;
(2)连接EM并延长交BC于F,证明△EDM≌△FBM,运用线段的等量代换即可求解;
(3)延长ED交BC于点F,连接AF、MF,结合矩形的性质和等腰直角三角形性质,合理运用角的等量代换即可求解.
解答 解:(1)MN⊥EC,MN=$\frac{1}{2}$EC;
由等腰Rt△ABC和等腰Rt△AED中,∠ACB=∠AED=90°,
可知,AE=BE=EC,DE⊥AB,
∵点M、N分别是DB、EC的中点,
∴MN∥AB,且MN=$\frac{1}{2}$BE,
∴MN⊥EC,MN=$\frac{1}{2}$EC;
(2)如图2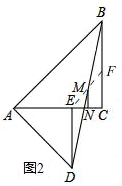
连接EM并延长交BC于F,
∵∠AED=∠ACB=90°,
∴DE∥BC,
∴∠DEM=∠AFM,∠EDM=∠MBF,
又BM=MD,
在△EDM和△FBM中,
$\left\{\begin{array}{l}{∠DEM=∠AFM}\\{∠EDM=∠MBF}\\{BM=MD}\end{array}\right.$,
∴△EDM≌△FBM,
∴BF=DE=AE,EM=FM,
∴MN=$\frac{1}{2}$FC=$\frac{1}{2}$(BC-BF)=$\frac{1}{2}$(AC-AF)=$\frac{1}{2}$EC,
且MN⊥EC;
(3)如图3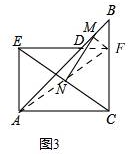
延长ED交BC于点F,连接AF、MF,则AF为矩形ACFE对角线,所以必经过EC的中点N且AN=NF=EN=NC.
在Rt△BDF中,M是BD的中点,∠B=45°,
∴FD=FB,
∴FM⊥AB,
∴MN=NA=NF=NC,
即MN=$\frac{1}{2}$EC,
∴∠NAM=∠AMN,∠NAC=∠NCA,
∴∠MNF=∠NAM+∠AMN=2∠NAM,∠FNC=∠NAC+∠NCA=2∠NAC,
∴∠MNC=∠MNF+∠FNC=2∠NAM+2∠NAC=2(∠NAM+∠NAC)=2∠DAC=90°,
∴∠MNC=90°,
即MN⊥EC且MN=$\frac{1}{2}$EC.
点评 此题主要考查集几何变换,熟悉全等三角形的证明和矩形的性质,会灵活运用等腰直角三角形的性质进行解题,能抓住在图形变换中的不变关系是解题的关键.

 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案| A. | 1 | B. | -1 | C. | 2-$\sqrt{3}$ | D. | $\sqrt{3}-2$ |
 如图,在?ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为4cm.
如图,在?ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为4cm.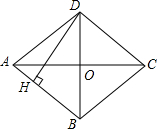 如图,四边形ABCD是菱形,对角线AC=8cm,BD=6 cm,DH⊥AB于H,DH的长是$\frac{24}{5}$cm.
如图,四边形ABCD是菱形,对角线AC=8cm,BD=6 cm,DH⊥AB于H,DH的长是$\frac{24}{5}$cm.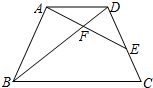 如图,在梯形ABCD中,AD∥BC,AB=CD=8,AD=6,E在边CD上,AE与BD相交于点F,∠EAD=∠ABD.
如图,在梯形ABCD中,AD∥BC,AB=CD=8,AD=6,E在边CD上,AE与BD相交于点F,∠EAD=∠ABD.