题目内容
4.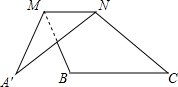 如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )
如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )| A. | 88° | B. | 116° | C. | 126° | D. | 112° |
分析 由MN∥BC,可得出∠MNC与∠C互补,由三角形的内角和为180°可求出∠C的度数,从而得出∠MNC的度数,由折叠的性质可知∠A′NM与∠MNC互补,而∠A′NC=∠MNC-∠A′NM,套入数据即可得出结论.
解答 解:∵MN∥BC,
∴∠MNC+∠C=180°,
又∵∠A+∠B+∠C=180°,∠A=28°,∠B=120°,
∴∠C=32°,∠MNC=148°.
由折叠的性质可知:∠A′NM+∠MNC=180°,
∴∠A′NM=32°,
∴∠A′NC=∠MNC-∠A′NM=148°-32°=116°.
故选B.
点评 本题考查平行线的性质、折叠的性质以及三角形的内角和为180°,解题的关键是找出∠MNC与∠A′NM的度数.本题属于基础题,难度不大,根据平行线的性质找出角的关系,结合图形即可得出结论.

练习册系列答案
相关题目
12.若m=2+$\sqrt{3}$,n=2-$\sqrt{3}$,则m2013•n2014的值为( )
| A. | 1 | B. | -1 | C. | 2-$\sqrt{3}$ | D. | $\sqrt{3}-2$ |
9.一个多边形的内角和是外角和的n倍(n是正整数),则该多边形的边数是( )
| A. | 2n+2 | B. | n+1 | C. | 2n+1 | D. | 2n+4 |
 如图,在?ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为4cm.
如图,在?ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为4cm.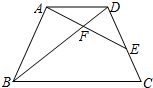 如图,在梯形ABCD中,AD∥BC,AB=CD=8,AD=6,E在边CD上,AE与BD相交于点F,∠EAD=∠ABD.
如图,在梯形ABCD中,AD∥BC,AB=CD=8,AD=6,E在边CD上,AE与BD相交于点F,∠EAD=∠ABD.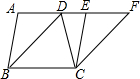 如图,在四边形ABCD中,AD∥BC,且AD<BC,连接BD,现将三角形ABD平移到三角形ECF的位置.
如图,在四边形ABCD中,AD∥BC,且AD<BC,连接BD,现将三角形ABD平移到三角形ECF的位置. 已知:如图,在?ABCD中,点E、F在AC上,且AE=CF.求证:四边形EBFD是平行四边形.
已知:如图,在?ABCD中,点E、F在AC上,且AE=CF.求证:四边形EBFD是平行四边形.