题目内容
7.对于平面直角坐标系中任意两点M(x1,y1),N(x2,y2),称|x1-x2|+|y1-y2|为M,N两点的直角距离,记作:d(M,N).如:M(2,-3),N(1,4),则d(M,N)=|2-1|+|-3-4|=8.若P(x0,y0)是一定点,Q(x,y)是直线y=kx+b上的一动点,称d(P,Q)的最小值为P到直线y=kx+b的直角距离.则P(0,-3)到直线x=1的直角距离为( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 先找出P(0,-3)到直线x=1最近的点的坐标,再根据直角距离公式即可得出结论.
解答 解:∵垂线段最短,
∴P(0,-3)到直线x=1最近的点的坐标为(1,-3),
∴|0-1|+|-3+3|=1.
故选D.
点评 本题考查的是一次函数图象上上点的坐标特点,正确理解直角距离的定义是解答此题的关键.

练习册系列答案
相关题目
18.把抛物线y=-2x2+1向左平移1个单位,然后向上平移3个单位,则平移后抛物线的顶点坐标是( )
| A. | (-1,-4) | B. | (-1,4) | C. | (1,-4) | D. | (1,4) |
2.若$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{2x+y=m}\\{x-ny=3}\end{array}\right.$的解,则m,n的值为( )
| A. | 3,1 | B. | 3,-1 | C. | -3,1 | D. | -3,-1 |
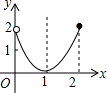
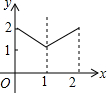
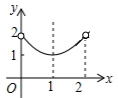
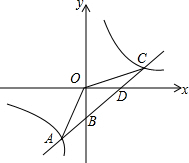 如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D. 在坐标系中,点A的坐标为(3,0),点P是y轴右侧一点,且AP=2,点B上直线y=x+1上一动点,且PB⊥AP于点P,则tan∠ABP=m,则m的取值范围是0<m≤1.
在坐标系中,点A的坐标为(3,0),点P是y轴右侧一点,且AP=2,点B上直线y=x+1上一动点,且PB⊥AP于点P,则tan∠ABP=m,则m的取值范围是0<m≤1.