题目内容
15.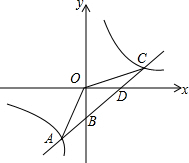 如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.(1)求一次函数y1=kx+b与反比例函数y2=$\frac{m}{x}$的函数关系式;
(2)连结OA、OC,求△AOC的面积;
(3)当x取何值时y1=kx+b的值大于反比例函数y2=$\frac{m}{x}$的值.
分析 (1)把A的坐标代入反比例函数的解析式求出m,把C的坐标代入反比例函数解析式求出n,把A、C的坐标代入一次函数的解析式得出方程组,求出方程组的解即可;
(2)求出一次函数与x轴的交点坐标,的OD值,根据三角形的面积公式求出即可;
(3)结合图象和A、C的坐标即可求出答案.
解答 (1)解:∵把A(-2,-5)代入代入y2=$\frac{m}{x}$,得:m=10,
∴y2=$\frac{10}{x}$,
∵把C(5,n)代入得:n=2,
∴C(5,2),
∵把A、C的坐标代入y1=kx+b得:
$\left\{\begin{array}{l}{-2k+b=-5}\\{5k+b=2}\end{array}\right.$,
解得:k=1,b=-3,
∴y1=x-3,
答:反比例函数的表达式是y2=$\frac{10}{x}$,一次函数的表达式是y1=x-3; (2)解:∵把y=0代入y1=x-3得:x=3,
(2)解:∵把y=0代入y1=x-3得:x=3,
∴D(3,0),OD=3,
∴S△AOC=S△DOC+S△AOD
=$\frac{1}{2}$×3×2+$\frac{1}{2}$×3×|-5|
=10.5,
答:△AOC的面积是10.5;
(3)解:根据图象和A、C的坐标得出,当-2<x<0或x>5时,y1=kx+b的值大于反比例函数y2=$\frac{m}{x}$的值.
点评 本题考查了用待定系数法求一次函数与反比例函数的解析式,一次函数与反比例函数图象上点的坐标特征,三角形的面积,一次函数与反比例函数的交点问题的应用,主要考查学生运用性质进行计算的能力,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
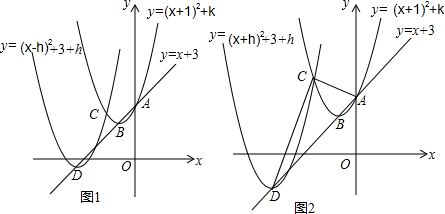
 如图所示,在平面内有四个点,它们的坐标分别是A(-1,0),B(2+$\sqrt{3}$,0),C(2,1),D(0,1).
如图所示,在平面内有四个点,它们的坐标分别是A(-1,0),B(2+$\sqrt{3}$,0),C(2,1),D(0,1).