题目内容
17．如图，正方形纸片ABCD的边长为2，翻折∠B、∠D，使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕（如图2）．设BE=x（0＜x＜2），阴影部分面积为y，则y与x之间的函数图象为（ ）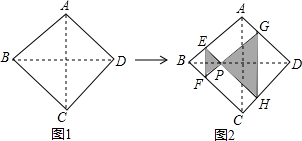
| A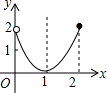． |  | B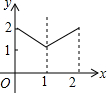． |  | C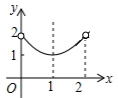． |  | D． |  |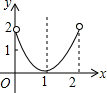
分析 阴影部分的面积=△EFP的面积+△GHP的面积．得出函数关系式，进而判断即可．
解答 解：阴影部分的面积=阴影部分的面积=△EFP的面积+△GHP的面积
∵AE=x，
∴阴影部分的面积=$\frac{1}{2}$x•x+$\frac{1}{2}$×（2-x）•（2-x）=x2-2x+2=（x-1）2+1 （0＜x＜2），
它的图象为C．
故选C．
点评 此题考查了正方形的性质，本题关键是利用分割法求出阴影部分面积，利用二次函数的知识解决问题，属于中考常考题型．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
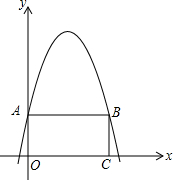如图，矩形AOCB的两边在坐标轴上，抛物线y=-x2+4x+2经过A、B两点．
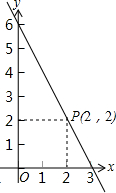函数y=-2x+6的图象如图所示，P（2，2）是图象上的一点，观察图象回答问题．