题目内容
8.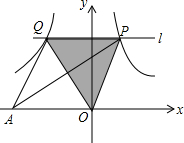 如图,在平面直角坐标系中,直线l∥x轴,且直线l分别与反比例函数y=$\frac{6}{x}$(x>0)和y=-$\frac{8}{x}$(x<0)的图象交于点P、Q,连结PO、QO,则△PAQ的面积为7.
如图,在平面直角坐标系中,直线l∥x轴,且直线l分别与反比例函数y=$\frac{6}{x}$(x>0)和y=-$\frac{8}{x}$(x<0)的图象交于点P、Q,连结PO、QO,则△PAQ的面积为7.
分析 根据题意可以分别设出点Q和点P的坐标,然后根据直线l分别与反比例函数y=$\frac{6}{x}$(x>0)和y=-$\frac{8}{x}$(x<0)的图象交于点P、Q,可以分别求得点P和点Q的横纵坐标的乘积,从而可以得到△PAQ的面积.
解答 解:设点P的坐标为(a,b),点Q的坐标为(c,d),
∵直线l分别与反比例函数y=$\frac{6}{x}$(x>0)和y=-$\frac{8}{x}$(x<0)的图象交于点P、Q,
∴ab=6,cd=-8,
∴${S}_{△PQO}=\frac{-c•d}{2}+\frac{a•b}{2}=\frac{8}{2}+\frac{6}{2}$=4+3=7.
故答案为:7.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,找出所求问题需要的条件,明确反比例函数的特点.

练习册系列答案
相关题目
9.?ABCD中,∠A=4∠B,则∠D的度数是( )
| A. | 18° | B. | 36° | C. | 72° | D. | 144° |
17.点P为直线l外一点,点A、B、C为l上三点,PA=5cm,PB=6cm,PC=6cm,则点P到直线l的距离是( )
| A. | 5cm | B. | 小于5cm | C. | 不大于5cm | D. | 7cm |
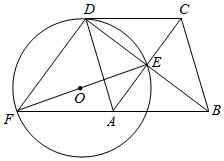 如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O.
如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O.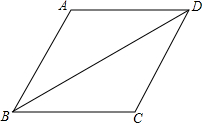 如图,菱形ABCD的周长为20,对角线BD=8,求sin∠ABD的值.
如图,菱形ABCD的周长为20,对角线BD=8,求sin∠ABD的值.