题目内容
6.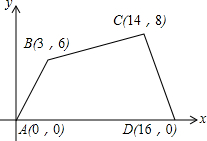 如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),
如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),(1)求四边形ABCO的面积.
(2)如果把原来ABCD各个顶点纵坐标保持不变,横坐标增加2,所得的四边形有什么变化?如下变化:纵坐标不变,横坐标减2,并所得的图案与原来相比有什么变化?面积又是多少?(不画图直接回答)
分析 (1)直接利用四边形面积求法将原图形分割求出答案;
(2)直接利用平移的性质分析得出答案.
解答 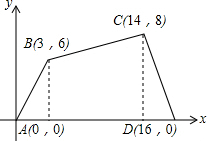 解:(1)四边形ABCO的面积为:$\frac{1}{2}$×3×6+$\frac{1}{2}$(6+8)×11+$\frac{1}{2}$×2×8=94;
解:(1)四边形ABCO的面积为:$\frac{1}{2}$×3×6+$\frac{1}{2}$(6+8)×11+$\frac{1}{2}$×2×8=94;
(2)因为原来四边形ABCD各个顶点纵坐标保持不变,横坐标增加2,
就是把四边形ABCD向右平移2个单位,所以,所得的四边形面积不变;
当纵坐标不变,横坐标减2,并所得的图案与原来相比形状大小都不变,面积是:94.
点评 此题主要考查了坐标与图形的性质,正确利用平移的性质分析是解题关键.

练习册系列答案
相关题目
17.点P为直线l外一点,点A、B、C为l上三点,PA=5cm,PB=6cm,PC=6cm,则点P到直线l的距离是( )
| A. | 5cm | B. | 小于5cm | C. | 不大于5cm | D. | 7cm |
16.下列各式是最简二次根式的是( )
| A. | $\sqrt{32}$ | B. | $\sqrt{\frac{8}{9}}$ | C. | $\sqrt{15}$ | D. | $\frac{1}{\sqrt{2}}$ |
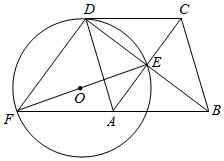 如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O.
如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O.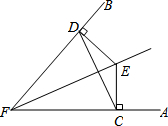 已知:E是∠AFB的平分线上一点,EC⊥FA,ED⊥FB,垂足分别为C、D.求证:FE是CD的垂直平分线.
已知:E是∠AFB的平分线上一点,EC⊥FA,ED⊥FB,垂足分别为C、D.求证:FE是CD的垂直平分线.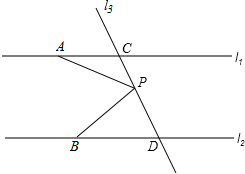 已知直线l1∥l2,A是l1上一点,B是l2上一点,直线l3和直线l1,l2交于点C和D,在直线CD上有一点P
已知直线l1∥l2,A是l1上一点,B是l2上一点,直线l3和直线l1,l2交于点C和D,在直线CD上有一点P