题目内容
9.(1)若函数y=(k+1)x+k2-1是正比例函数,求k的值;(2)若一次函数y=kx+b的图象与正比例函数y=2x的图象平行,且经过点A(1,-2),求一次函数的解析式;
(3)若y=(2m-1)x${\;}^{{m}^{2}-3}$是正比例函数,且y随x的增大而减小,求m的值.
分析 (1)先根据正比例函数的定义列出关于k的方程组,求出k的值即可;
(2)根据平行线的性质得出k=2,中把A的坐标代入求出b=-4即可;
(3)根据正比例函数的定义和性质列出关于k的不等式组,求出k的值即可.
解答 解:∵函数y=(k+1)x+k2-1是正比例函数,
∴$\left\{\begin{array}{l}{k+1≠0}\\{{k}^{2}-1=0}\end{array}\right.$,
解得k=1.
(2)根据题意得:k=2,
∴y=2x+b,
把A(1,-2)代入得:2+b=-2,
解得:b=-4,
∴一次函数的解析式为y=2x-4;
(3)∵若y=(2m-1)x${\;}^{{m}^{2}-3}$是正比例函数,且y随x的增大而减小,
∴$\left\{\begin{array}{l}{{m}^{2}-3=1}\\{2m-1<0}\end{array}\right.$,
解得:m=-2.
点评 本题考查的是正比例函数的定义和性质以及平行线的性质,熟记形如y=kx(k≠0)的函数叫正比例函数是关键.

练习册系列答案
相关题目
20.某超市进了一批货,出售时要在进价的基础上加一定的利润,其销售量x(千克)与销售价c(元)之间的关系如下表:
(1)试用含有x的代数式表示售价c;
(2)若小华的妈妈想买8千克这种货物,那么她需要付多少钱?
(1)试用含有x的代数式表示售价c;
(2)若小华的妈妈想买8千克这种货物,那么她需要付多少钱?
| 销售量x(千克) | 销售价c(元) |
| 1 | 2+0.1 |
| 2 | 4+0.2 |
| 3 | 6+0.3 |
| 4 | 8+0.4 |
| … | … |
17.如果某个三角形的三个内角之比为1:2:1,那么这个三角形是( )
| A. | 等腰直角三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰三角形 |
14.在△ABC中,已知∠A=∠B=$\frac{1}{2}$∠C,则三角形是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
1.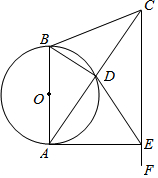 如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.
(1)试说明:△CBA∽△CDE;
(2)若AB=3,BD=2,求AE的长.
 如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.(1)试说明:△CBA∽△CDE;
(2)若AB=3,BD=2,求AE的长.
19.下列各数中是用科学记数法表示的是( )
| A. | 0.58×105 | B. | 12.3×107 | C. | 12×103 | D. | 8.0×108 |
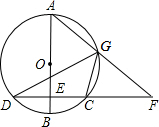 已知:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,G是弧AC上的任意一点,AG、DC的延长线相交于点F.
已知:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,G是弧AC上的任意一点,AG、DC的延长线相交于点F. 将连续的奇数1,3,5,7,9…,排成如下的数表:
将连续的奇数1,3,5,7,9…,排成如下的数表: