题目内容
11. 如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连接AA′,∠1=26°,则∠B的度数是71°.
如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连接AA′,∠1=26°,则∠B的度数是71°.
分析 根据旋转的性质可得AC=A′C,然后判断出△ACA′是等腰直角三角形,根据等腰直角三角形的性质可得∠CAA′=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠A′B′C,然后根据旋转的性质可得∠B=∠A′B′C.
解答 解:∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,
∴AC=A′C,
∴△ACA′是等腰直角三角形,
∴∠CAA′=45°,
∴∠A′B′C=∠1+∠CAA′=26°+45°=71°,
由旋转的性质得∠B=∠A′B′C=71°.
故答案为:71°.
点评 本题考查了旋转的性质,等腰直角三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
12. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )| A. | 50° | B. | 40° | C. | 30° | D. | 25° |
6.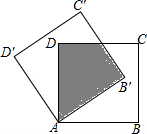 如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2$\sqrt{3}$cm,则图中阴影部分的面积为( )
如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2$\sqrt{3}$cm,则图中阴影部分的面积为( )
 如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2$\sqrt{3}$cm,则图中阴影部分的面积为( )
如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2$\sqrt{3}$cm,则图中阴影部分的面积为( )| A. | 6cm2 | B. | (12-6$\sqrt{3}$)cm2 | C. | 3$\sqrt{3}$cm2 | D. | 4$\sqrt{3}$cm2 |
 点A,B在数轴上的位置如图所示,点P是数轴上的一动点.
点A,B在数轴上的位置如图所示,点P是数轴上的一动点. 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4)、B(-2,1)、C(-5,2).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4)、B(-2,1)、C(-5,2). 某校240名学生参加“献爱心”义务捐款活动.要求每人捐4-7元,(捐款数
某校240名学生参加“献爱心”义务捐款活动.要求每人捐4-7元,(捐款数