题目内容
7. 如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则AC的长为$\frac{2\sqrt{10}}{3}$.
如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则AC的长为$\frac{2\sqrt{10}}{3}$.
分析 将正方体展开,右边与后面的正方形与前面正方形放在一个面上,此时AB最短,根据三角形MCB与三角形ACN相似,由相似得比例得到MC=2NC,求出CN的长,利用勾股定理求出AC的长即可.
解答  解:将正方体展开,右边与后面的正方形与前面正方形放在一个面上,展开图如图所示,此时AB最短,
解:将正方体展开,右边与后面的正方形与前面正方形放在一个面上,展开图如图所示,此时AB最短,
∵△BCM∽△ACN,
∴$\frac{MB}{AN}$=$\frac{MC}{NC}$,即$\frac{4}{2}$=$\frac{MC}{NC}$=2,即MC=2NC,
∴CN=$\frac{1}{3}$MN=$\frac{2}{3}$,
在Rt△ACN中,根据勾股定理得:AC=$\sqrt{A{N}^{2}+C{N}^{2}}$=$\frac{2\sqrt{10}}{3}$,
故答案为:$\frac{2\sqrt{10}}{3}$.
点评 此题考查了平面展开-最短路径问题,涉及的知识有:相似三角形的判定与性质,勾股定理,熟练求出CN的长是解本题的关键.

练习册系列答案
相关题目
18.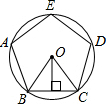 如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
 如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )| A. | R2-r2=a2 | B. | a=2Rsin36° | C. | a=2rtan36° | D. | r=Rcos36° |
12. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )| A. | 50° | B. | 40° | C. | 30° | D. | 25° |
19.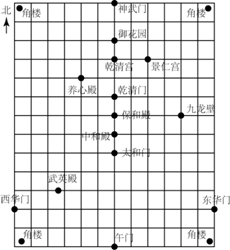 如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
 如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )| A. | 景仁宫(4,2)? | B. | 养心殿(-2,3) | C. | 保和殿(1,0) | D. | 武英殿(-3.5,-4) |
6.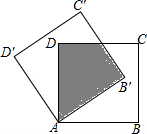 如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2$\sqrt{3}$cm,则图中阴影部分的面积为( )
如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2$\sqrt{3}$cm,则图中阴影部分的面积为( )
 如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2$\sqrt{3}$cm,则图中阴影部分的面积为( )
如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2$\sqrt{3}$cm,则图中阴影部分的面积为( )| A. | 6cm2 | B. | (12-6$\sqrt{3}$)cm2 | C. | 3$\sqrt{3}$cm2 | D. | 4$\sqrt{3}$cm2 |
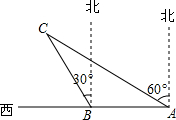 如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:$\sqrt{3}$≈1.732)
如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:$\sqrt{3}$≈1.732) 如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.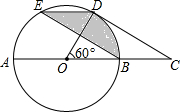 如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为$\widehat{AD}$的中点,连接DE,EB.
如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为$\widehat{AD}$的中点,连接DE,EB.