题目内容
6. 已知平面直角坐标系中,开口向上的抛物线与x轴交于A(2,0)、B(4,0)两点,设抛物线的顶点为M,∠AMB=90°.
已知平面直角坐标系中,开口向上的抛物线与x轴交于A(2,0)、B(4,0)两点,设抛物线的顶点为M,∠AMB=90°.(1)求该抛物线的解析式;
(2)过点C(0,3)作x轴的平行线,交抛物线于E、F,交其对称轴于D
①求证:OD∥AF;
②在OE的右侧作OP=OE,在AF的左侧作AQ=OF,且∠EOP=∠FAQ,求证:DP=DQ.
分析 (1)根据题目中的信息可以得到顶点M的坐标,然后根据抛物线与x轴交于A(2,0)、B(4,0)两点,从而可以求得抛物线的解析式;
(2)①要证明OD∥AF,只要证明四边形OAFD是平行四边形即可,根据题意可以求得点E和点F的坐标,从而可以求得DF的长,从而可以证明结论成立;
②要证明DP=DQ,只要证明△POD≌△DAQ即可,根据题目中的条件可以找到证明两个三角形全等的条件,本题得以解决.
解答 解:(1)∵抛物线与x轴交于A(2,0)、B(4,0)两点,抛物线的顶点为M,∠AMB=90°,
∴点M的横坐标是3,AB=4-2=2,
∴点M的纵坐标是-1,
∴点M(3,-1),
设抛物线的解析式为y=a(x-3)2-1,
∴0=a(2-3)2-1,得a=1,
∴y=(x-3)2-1=x2-6x+8,
即该抛物线的解析式是y=x2-6x+8;
(2)①证明:∵点C(0,3),
将y=3代入y=x2-6x+8,得x1=1,x2=5,
∴点E(1,3),点F(5,3),
∴DF=5-3=2,
∵OA=2,
∴OA=DF,
∵OA∥DF,
∴四边形OAFD是平行四边形,
∴OD∥AF;
②证明:连接OD,如右图所示,
同理可得,DE=3-1=2,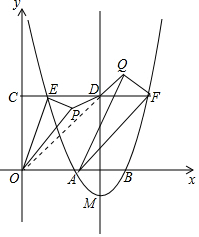
∴DE∥OA,DE=OA,
∴四边形OADE是平行四边形,
∴OE=AD,
又∵OE=OP,OD=AF,AF=AQ,
∴OP=AD,OD=AQ,
∵OE∥AD,OD∥AF,
∴∠EOB=∠DAB,∠DOB=∠FAB,
又∵∠EOP=∠FAQ,
∴∠POD=∠DAQ,
在△POD和△DAQ中,
$\left\{\begin{array}{l}{OP=AD}\\{∠POD=∠DAQ}\\{OD=AQ}\end{array}\right.$,
∴△POD≌△DAQ(SAS),
∴DP=QD,
即DP=DQ.
点评 本题考查二次函数综合题、全等三角形的证明、等腰直角三角形的性质,解答此类题目的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想、函数的性质和全等三角形的证明的相关知识解答.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )| A. | sinA=$\frac{BD}{BC}$ | B. | cosA=$\frac{AC}{AD}$ | C. | tanA=$\frac{CD}{AB}$ | D. | cosB=$\frac{AC}{AB}$ |
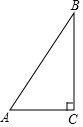 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )| A. | $\frac{36}{5}$ | B. | $\frac{12}{25}$ | C. | $\frac{9}{4}$ | D. | $\frac{3\sqrt{3}}{4}$ |
| 购票人数 | 1~50 | 51~100 | 100以上 |
| 每人门票价 | 12 | 10 | 8 |
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少元?
| A. | x=-2 | B. | x=3 | C. | x1=-2,x2=3 | D. | x1=2,x2=-3 |
 已知:如图,△ABC中,AB=AC,点D是△ABC内一点,且DB=DC,连接AD并延长,交BC于点E.
已知:如图,△ABC中,AB=AC,点D是△ABC内一点,且DB=DC,连接AD并延长,交BC于点E.
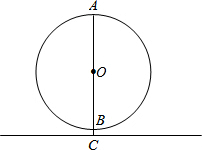 如图,⊙O是梦幻谷的摩天轮示意图,⊙O的最高处A到地面的距离是23米,最低处B到地面的距离是3米,AB是直径,摩天轮匀速转动,从B处乘坐绕摩天轮一周要6分钟,
如图,⊙O是梦幻谷的摩天轮示意图,⊙O的最高处A到地面的距离是23米,最低处B到地面的距离是3米,AB是直径,摩天轮匀速转动,从B处乘坐绕摩天轮一周要6分钟,