题目内容
1. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )| A. | sinA=$\frac{BD}{BC}$ | B. | cosA=$\frac{AC}{AD}$ | C. | tanA=$\frac{CD}{AB}$ | D. | cosB=$\frac{AC}{AB}$ |
分析 利用同角的余角相等可得∠A=∠BCD,再根据正弦定义可得答案.
解答 解:∵∠ACB=90°,CD⊥AB,
∴∠A+∠DCA=90°,∠DCA+∠BCD=90°,
∴∠A=∠BCD,
∴sinA=sin∠BCD=$\frac{BD}{BC}$,
故选:A.
点评 此题主要考查了锐角三角函数定义,关键是掌握正弦:锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.

练习册系列答案
相关题目
10.若ab>0,ac<0,则关于x的一元二次方程ax2+bx+c=0的根的叙述正确的是( )
| A. | 方程没有实数根 | |
| B. | 方程有两个不相等的正实数根或有两个不相等的负实数根 | |
| C. | 方程有一个正实数根和一个负实数根,且正实数根的绝对值较大 | |
| D. | 方程有一个正实数根和一个负实数根,且负实数根的绝对值较大 |

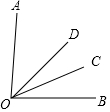 如图,OD是∠AOB的平分线,∠AOC=3∠BOC,∠COD=21°.
如图,OD是∠AOB的平分线,∠AOC=3∠BOC,∠COD=21°. 已知平面直角坐标系中,开口向上的抛物线与x轴交于A(2,0)、B(4,0)两点,设抛物线的顶点为M,∠AMB=90°.
已知平面直角坐标系中,开口向上的抛物线与x轴交于A(2,0)、B(4,0)两点,设抛物线的顶点为M,∠AMB=90°.