题目内容
11.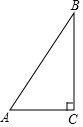 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )| A. | $\frac{36}{5}$ | B. | $\frac{12}{25}$ | C. | $\frac{9}{4}$ | D. | $\frac{3\sqrt{3}}{4}$ |
分析 首先根据勾股定理求出斜边AB的长,再根据三角形的面积为定值即可求出则点C到AB的距离.
解答 解:设点C到AB的距离为h,
在Rt△ABC中,∠C=90°,则有AC2+BC2=AB2,
∵AC=9,BC=12,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=15,
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•h,
∴h=$\frac{12×9}{15}$=$\frac{36}{5}$.
故选A.
点评 本题考查了勾股定理在直角三角形中的应用,解本题的关键是正确的运用勾股定理,确定AB为斜边.

练习册系列答案
相关题目
1.下列计算正确的是( )
| A. | ${({-\sqrt{2}})^2}$=2 | B. | $\sqrt{{{({-5})}^2}}$=-5 | C. | $\sqrt{2}÷\sqrt{6}=\sqrt{3}$ | D. | $\sqrt{{a^2}b}=a\sqrt{b}({a<0})$ |
19.下列等式一定成立的是( )
| A. | a2+a3=a5 | B. | a6÷a3=a2 | C. | (2xy2)3=6x3y6 | D. | (-xy)5÷(-xy)2=-x3y3 |
3. 如图,A,B是数轴上两点,过点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,若点P所表示的数是$\sqrt{13}$-2,则点A表示的数是( )
如图,A,B是数轴上两点,过点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,若点P所表示的数是$\sqrt{13}$-2,则点A表示的数是( )
 如图,A,B是数轴上两点,过点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,若点P所表示的数是$\sqrt{13}$-2,则点A表示的数是( )
如图,A,B是数轴上两点,过点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,若点P所表示的数是$\sqrt{13}$-2,则点A表示的数是( )| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
20.如果将“收入100元”记作“+100元”,那么“支出50元”应记作( )
| A. | +50元 | B. | -50元 | C. | +150元 | D. | -150元 |
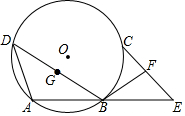 如图,点A、B、C、D在⊙O上,且$\widehat{AD}$=$\widehat{BC}$,E是AB延长线上一点,且BE=AB,F是EC的中点.
如图,点A、B、C、D在⊙O上,且$\widehat{AD}$=$\widehat{BC}$,E是AB延长线上一点,且BE=AB,F是EC的中点. 已知平面直角坐标系中,开口向上的抛物线与x轴交于A(2,0)、B(4,0)两点,设抛物线的顶点为M,∠AMB=90°.
已知平面直角坐标系中,开口向上的抛物线与x轴交于A(2,0)、B(4,0)两点,设抛物线的顶点为M,∠AMB=90°.
 在一次课外实践活动中,同学们要测量某公园人工湖两侧A、B两个凉亭之间的距离.现测得AC=300m,BC=700m,∠CAB=120°,请计算A、B两个凉亭之间的距离.
在一次课外实践活动中,同学们要测量某公园人工湖两侧A、B两个凉亭之间的距离.现测得AC=300m,BC=700m,∠CAB=120°,请计算A、B两个凉亭之间的距离.