题目内容
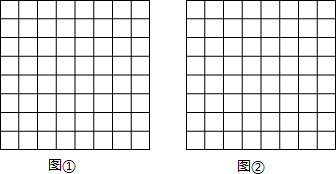
18.如图,正方形网格中的每个正方形的边长都是1,请在图中分别画出符合要求的图形,所画图形各顶点必须与网格中的小正方形顶点重重合,具体要求如下:(1)在图①中画一个三角形,使其三边长分别为3,2$\sqrt{2}$,$\sqrt{5}$.
(2)在图②中画一个三角形.使其周长为$\sqrt{10}$+$\sqrt{5}$+$\sqrt{17}$.
分析 (1)由勾股定理得出3、$\sqrt{5}$=$\sqrt{{1}^{2}+{2}^{2}}$、2$\sqrt{2}$=$\sqrt{{2}^{2}+{2}^{2}}$,即可画出图形;
(2)由勾股定理得出$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$、$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$、$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,即可画出图形.
解答 解:(1)如图①,AB=3,AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,BC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴△ABC即为所求作三角形;
(2)如图②,∵DE=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,DF=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,EF=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
∴△DEF的周长为$\sqrt{10}$+$\sqrt{5}$+$\sqrt{17}$,
故△DEF即为所求作三角形.
点评 本题考查了勾股定理,熟练掌握勾股定理,根据边长画出三角形是解决问题的关键.

练习册系列答案
相关题目
13.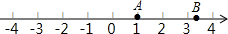 如图,在数轴上表示A,B两点对应的数分别是1,$\sqrt{10}$,则点B关于点A的对称点表示的数是( )
如图,在数轴上表示A,B两点对应的数分别是1,$\sqrt{10}$,则点B关于点A的对称点表示的数是( )
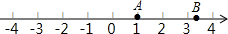 如图,在数轴上表示A,B两点对应的数分别是1,$\sqrt{10}$,则点B关于点A的对称点表示的数是( )
如图,在数轴上表示A,B两点对应的数分别是1,$\sqrt{10}$,则点B关于点A的对称点表示的数是( )| A. | -$\sqrt{10}$ | B. | -1-$\sqrt{10}$ | C. | $\sqrt{10}$-2 | D. | 2-$\sqrt{10}$ |
8.若a3•am=a5÷an,则m与n之间的关系是( )
| A. | m+n=-2 | B. | m+n=2 | C. | mn=$\frac{5}{3}$ | D. | mn=15 |

 a、b、c三点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{{b}^{2}-2bc+{c}^{2}}$.
a、b、c三点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{{b}^{2}-2bc+{c}^{2}}$.