题目内容
6. a、b、c三点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{{b}^{2}-2bc+{c}^{2}}$.
a、b、c三点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{{b}^{2}-2bc+{c}^{2}}$.
分析 根据数轴判断出a、b、c的正负情况,再根据二次根式的性质和绝对值的性质化简即可.
解答 解:由图可知,a<0,b<0,c>0,
所以,a+b<0,b-c<0,
$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{{b}^{2}-2bc+{c}^{2}}$,
=-a-(-a-b)+$\sqrt{(b-c)^{2}}$,
=-a+a+b+c-b,
=c.
点评 本题考查了实数与数轴,二次根式的性质,绝对值的性质,观察图形准确判断出a、b、c的正负情况是解题的关键.

练习册系列答案
相关题目
3.计算(a-3)2的结果是( )
| A. | a2-9 | B. | a2+9 | C. | a2-6a+9 | D. | a2+6a+9 |
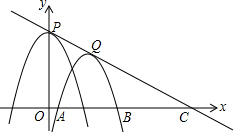 如图,点P是抛物线y=-x2+4的顶点,将抛物线平移,平移后的抛物线与x轴交于A,B两点(A在B的左侧)顶点Q落在第一象限内,且△ABQ是等边三角形,直线PQ与x轴交于点C,若PQ=$\sqrt{3}$,则BC=3$\sqrt{2}$-$\sqrt{3}$.
如图,点P是抛物线y=-x2+4的顶点,将抛物线平移,平移后的抛物线与x轴交于A,B两点(A在B的左侧)顶点Q落在第一象限内,且△ABQ是等边三角形,直线PQ与x轴交于点C,若PQ=$\sqrt{3}$,则BC=3$\sqrt{2}$-$\sqrt{3}$.