题目内容
10. 如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )| A. | 65° | B. | 60° | C. | 55° | D. | 45° |
分析 根据线段垂直平分线的性质得到AD=DC,根据等腰三角形的性质得到∠C=∠DAC,求得∠DAC=30°,根据三角形的内角和得到∠BAC=95°,即可得到结论.
解答 解:由题意可得:MN是AC的垂直平分线,
则AD=DC,故∠C=∠DAC,
∵∠C=30°,
∴∠DAC=30°,
∵∠B=55°,
∴∠BAC=95°,
∴∠BAD=∠BAC-∠CAD=65°,
故选A.
点评 此题主要考查了线段垂直平分线的性质,三角形的内角和,正确掌握线段垂直平分线的性质是解题关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
1.下列分式中,最简分式是( )
| A. | $\frac{{x}^{2}-1}{{x}^{2}+1}$ | B. | $\frac{x+1}{{x}^{2}-1}$ | ||
| C. | $\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-xy}$ | D. | $\frac{{x}^{2}-36}{2x+12}$ |
18.下列一元二次方程没有实数根的是( )
| A. | x2+2x+1=0 | B. | x2+x+2=0 | C. | x2-1=0 | D. | x2-2x-1=0 |
15. 《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )
 《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )| A. | 3步 | B. | 5步 | C. | 6步 | D. | 8步 |
2.某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
| 第1天 | 第2天 | 第3天 | 第4天 | |
| 售价x(元/双) | 150 | 200 | 250 | 300 |
| 销售量y(双) | 40 | 30 | 24 | 20 |
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
19.图(一)、图(二)分别为甲、乙两班学生参加投篮测验的投进球数直方图.若甲、乙两班学生的投进球数的众数分别为a、b;中位数分别为c、d,则下列关于a、b、c、d的大小关系,何者正确?( )

| A. | a>b,c>d | B. | a>b,c<d | C. | a<b,c>d | D. | a<b,c<d |
20.已知关于x的一元二次方程x2+2x-(m-2)=0有实数根,则m的取值范围是( )
| A. | m>1 | B. | m<1 | C. | m≥1 | D. | m≤1 |
 如图,AB∥DE,∠C=20°,∠B:∠D=4:3,则∠BOE=100度.
如图,AB∥DE,∠C=20°,∠B:∠D=4:3,则∠BOE=100度.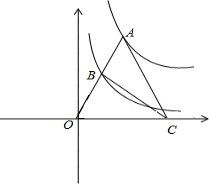 如图,点A为函数y=$\frac{9}{x}$(x>0)图象上一点,连结OA,交函数y=$\frac{1}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为6.
如图,点A为函数y=$\frac{9}{x}$(x>0)图象上一点,连结OA,交函数y=$\frac{1}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为6.