Question

5．阅读学习：
数学中有很多恒等式可以用图形的面积来得到．
如图1，可以求出阴影部分的面积是a²-b²；如图2，若将阴影部分裁剪下来，重新拼成一个矩形，它的长是a+b，宽是a-b，比较图1，图2阴影部分的面积，可以得到恒等式（a+b）（a-b）=a²-b²．

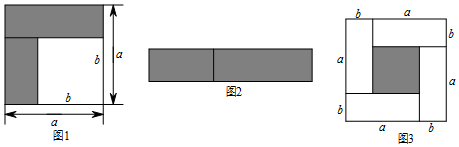
（1）观察图3，请你写出（a+b）²，（a-b）²，ab之间的一个恒等式（a-b）²=（a+b）²-ab．
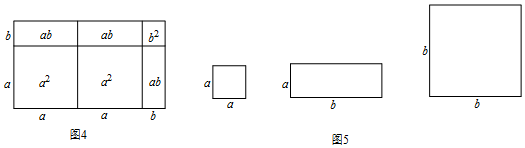
（2）观察图4，请写出图4所表示的代数恒等式：（2a+b）（a+b）=2a²+3ab+b²．
（3）现有若干块长方形和正方形硬纸片如图5所示，请你用拼图的方法推出一个恒等式（a+b）²=a²+2ab+b²，仿照图4画出你的拼图并标出相关数据．

Answer 1

分析 （1）利用完全平方公式找出（a+b）²、（a-b）²、ab之间的等量关系即可；
（2）根据面积的两种表达方式得到图4所表示的代数恒等式；
（3）由已知的恒等式，画出相应的图形即可．

解答 解：（1）（a+b）²，（a-b）²，ab之间的一个恒等式（a-b）²=（a+b）²-ab．
（2）图4所表示的代数恒等式：（2a+b）（a+b）=2a²+3ab+b²．
（3）如图所示：

故答案为：（a-b）²=（a+b）²-ab；（2a+b）（a+b）=2a²+3ab+b²．

点评 本题考查了完全平方公式的几何背景，根据矩形的面积公式分整体与部分两种思路表示出面积，然后再根据同一个图形的面积相等即可解答．