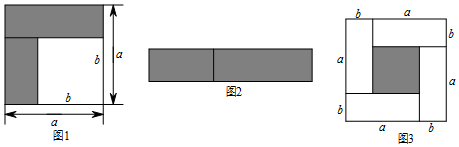
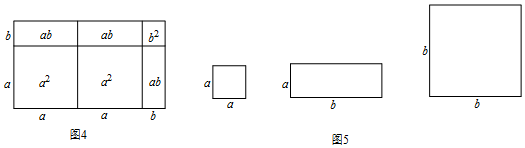
题目内容
15．如果我们要计算1+2+22+23+…+299+2100的值，我们可以用如下的方法：解：设S=1+2+22+23+…+299+2100?式
在等式两边同乘以2，则有2S=2+22+23+…+299+2100+2101?式
?式减去?式，得2S-S=2101-1
即 S=2101-1
即1+2+22+23+…+299+2100=2101-1
【理解运用】计算
（1）1+3+32+33+…+399+3100
（2）1-3+32-33+…-399+3100．
分析 （1）利用题中的方法求出原式的值即可；
（2）根据题中的方法利用加法即可．
解答 解：（1）设S=1+3+32+33+…+3100，①
①式两边都乘以3，得3S=3+32+33+…+3101，②
②-①得：2S=3101-1，即S=$\frac{{3}^{101}-1}{2}$，
则原式=$\frac{{3}^{101}-1}{2}$；
（2）设S=1-3+32-33+…+3100，①
①式两边都乘以3，得3S=3-32+33-…+3101，②
②+①得：4S=3101+1，即S=$\frac{{3}^{101}+1}{4}$，
则原式=$\frac{{3}^{101}+1}{4}$．
点评 本题考查了有理数的乘方，读懂题目信息，理解求和的运算方法是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
在平面直角坐标系中，点O是坐标原点，点A的坐标是（-a，a），点B的坐标是（c，b），满足$\left\{\begin{array}{l}{3a-b+2c=8}\\{a-2b-c=-4}\end{array}\right.$．
如图，在△ABC中，AD⊥BC于点D，AD=BC，以AB为底边作等腰Rt△ABE，连接ED，EC，延长CE交AD于点F，下列结论：①△ADE≌△BCE；②BD+DF=AD；③CE⊥DE；④S△BDE=S△ACE，其中正确的有①②③④（填写正确的番号）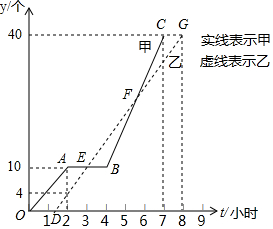
某车间甲、乙两名工人分别生产同种零件，他们生产的零件数量y（个）与生产时间t（小时）之间的关系如图所示（其中实线表示甲，虚线表示乙，且甲因机器故障停产了一段时间）．
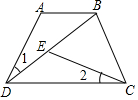如图，在四边形中ABCD中，AB∥CD，∠1=∠2，DB=DC，
