题目内容
15.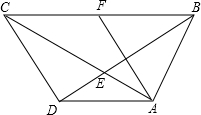 如图,在四边形ABCD中,AB=AD,AC与BD相交于点E,∠ADB=∠ACB.
如图,在四边形ABCD中,AB=AD,AC与BD相交于点E,∠ADB=∠ACB.求证:AD2=AE•AC.
分析 由AB=AD,利用等边对等角得到一对角相等,再由已知角相等,等量代换得到∠ABD=∠ACB,再由一对公共角,得到三角形BAE与三角形CAB相似,由相似得比例,等量代换即可得证.
解答 证明:∵AB=AD,
∴∠ADB=∠ABD,
∵∠ADB=∠ACB,
∴∠ABD=∠ACB,
∵∠BAE=∠CAB,
∴△BAE∽△CAB,
∴$\frac{AB}{AC}$=$\frac{AE}{AB}$,即AB2=AC•AE,
∵AB=AD,
∴AD2=AC•AE;
点评 此题考查了相似三角形的判定与性质,等腰三角形的性质;熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
6.下列计算正确的是( )
| A. | $\sqrt{{5}^{2}}$=±5 | B. | $\sqrt{{(-5)}^{2}}$=-5 | C. | ${(2\sqrt{3})}^{2}$=12 | D. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ |
20.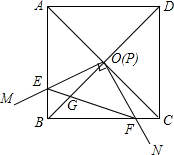 如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为α(0°<α<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,下列结论中错误的是( )
如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为α(0°<α<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,下列结论中错误的是( )
 如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为α(0°<α<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,下列结论中错误的是( )
如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为α(0°<α<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,下列结论中错误的是( )| A. | OF=OE | |
| B. | BE+BF=$\sqrt{2}$OA | |
| C. | 在旋转的过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{3}{4}$ | |
| D. | AE•BE=BO•BG. |
 在等边三角形ABC中,AB=9cm,点P从点C出发沿CB边向点B以2cm/s的速度移动,点Q从点B出发沿BA边向点A以5cm/s的速度移动,P、Q两点同时出发,它们移动的时间为ts.
在等边三角形ABC中,AB=9cm,点P从点C出发沿CB边向点B以2cm/s的速度移动,点Q从点B出发沿BA边向点A以5cm/s的速度移动,P、Q两点同时出发,它们移动的时间为ts.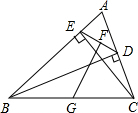 如图,BD、CE是△ABC不同边上的高,点G、F分别是BC、DE的中点,试证明GF⊥DE.
如图,BD、CE是△ABC不同边上的高,点G、F分别是BC、DE的中点,试证明GF⊥DE.