题目内容
17.点P(2a,1-3a)是第二象限内的一个点,且点P到两坐标轴的距离之和为4,则点P的坐标是(-$\frac{6}{5}$,$\frac{14}{5}$).分析 根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度列方程求出a的值,再求解即可.
解答 解:∵点P(2a,1-3a)是第二象限内的一个点,且点P到两坐标轴的距离之和为4,
∴-2a+1-3a=4,
解得a=-$\frac{3}{5}$,
∴2a=2×(-$\frac{3}{5}$)=-$\frac{6}{5}$,
1-3a=1-3×(-$\frac{3}{5}$)=1+$\frac{9}{5}$=$\frac{14}{5}$,
所以,点P的坐标为(-$\frac{6}{5}$,$\frac{14}{5}$).
故答案为(-$\frac{6}{5}$,$\frac{14}{5}$).
点评 本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列计算正确的是( )
| A. | $\sqrt{{5}^{2}}$=±5 | B. | $\sqrt{{(-5)}^{2}}$=-5 | C. | ${(2\sqrt{3})}^{2}$=12 | D. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ |
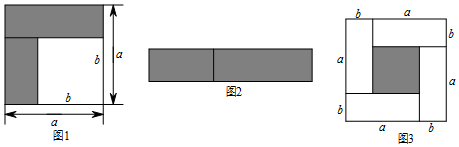
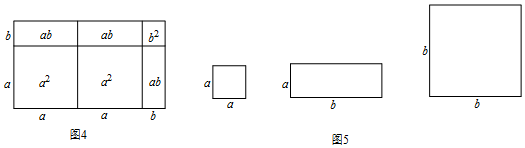
 如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.