题目内容
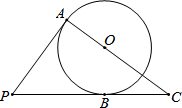 如图,PA、PB是⊙O的切线,切点分别为A、B,AO、PB的延长线相交于点C,⊙O的半径为3,BC=4,求切线PA的长.
如图,PA、PB是⊙O的切线,切点分别为A、B,AO、PB的延长线相交于点C,⊙O的半径为3,BC=4,求切线PA的长.考点:切线的性质
专题:计算题
分析:连结OB,如图,由于PA、PB是⊙O的切线,根据切线的性质和切线长定理得到AC⊥AB,OB⊥PC,PA=PB,再在Rt△OBC中利用勾股定理计算出OC=5,则AC=OA+OC=8,然后证明Rt△CBO∽Rt△CAP,再利用相似比可计算PA的长.
解答:解:连结OB,如图,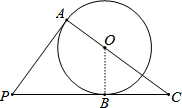
∵PA、PB是⊙O的切线,
∴AC⊥AB,OB⊥PC,PA=PB,
∴∠CAP=90°,∠OBC=90°,
在Rt△OBC中,OC=
=5,
∴AC=OA+OC=3+5=8,
而∠BCO=∠ACP,
∴Rt△CBO∽Rt△CAP,
∴
=
,即
=
,
∴PA=6.

∵PA、PB是⊙O的切线,
∴AC⊥AB,OB⊥PC,PA=PB,
∴∠CAP=90°,∠OBC=90°,
在Rt△OBC中,OC=
| OB2+BC2 |
∴AC=OA+OC=3+5=8,
而∠BCO=∠ACP,
∴Rt△CBO∽Rt△CAP,
∴
| OB |
| PA |
| BC |
| AC |
| 3 |
| PA |
| 4 |
| 8 |
∴PA=6.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,得到直角三角形.

练习册系列答案
相关题目
 如图,AB=AC=AD,且∠BDC=20°,则∠BAC的大小是( )
如图,AB=AC=AD,且∠BDC=20°,则∠BAC的大小是( )| A、30° | B、40° |
| C、45° | D、50° |
 如图,已知∠A=90°,∠B=15°,BD=DC,AC=4.求DB的长.
如图,已知∠A=90°,∠B=15°,BD=DC,AC=4.求DB的长.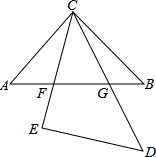 如图是两块等腰直角三角板放置在一起,AC=BC,∠ACB=90°,CE=DE,∠E=90°,CE交AB于F,CD交AB于G.求证:AF2+BG2=FG2.
如图是两块等腰直角三角板放置在一起,AC=BC,∠ACB=90°,CE=DE,∠E=90°,CE交AB于F,CD交AB于G.求证:AF2+BG2=FG2.