题目内容
观察按下列规则排成的一列数(已写出了第1至16个数):
;
,
;
,
,
;
,
,
,
;
,
,
,
,
;
,…
(1)依次规律,写出第17、18、19个数,分别为 ;
(2)若某一个数为
(a≥3的整数),请写出数
的前一个数为 ,
的后一个数为 ;
(3)在上面这列数中,从左起第m个数记为F(m),当F(m)=
时,求m的值和这m个数的积.
| 1 |
| 1 |
| 1 |
| 2 |
| 2 |
| 1 |
| 1 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
| 4 |
| 1 |
| 1 |
| 5 |
| 2 |
| 4 |
| 3 |
| 3 |
| 4 |
| 2 |
| 5 |
| 1 |
| 1 |
| 6 |
(1)依次规律,写出第17、18、19个数,分别为
(2)若某一个数为
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
(3)在上面这列数中,从左起第m个数记为F(m),当F(m)=
| 2 |
| 2001 |
考点:规律型:数字的变化类
专题:规律型
分析:(1)根据后一个数的分子比前一个数的分子大1,分母比前一个分数的分母小1依次写出即可;
(2)根据变化规律
前面的分数的分子减1,分母加1,后一个分数的分子加1,分母减1写出即可;
(3)观察不难发现,分子为2的分数的分母与前一组数的个数相同,然后列式计算即可求出m的值,再根据每一组数的乘积为1计算即可求出这m个数的积.
(2)根据变化规律
| 2 |
| a |
(3)观察不难发现,分子为2的分数的分母与前一组数的个数相同,然后列式计算即可求出m的值,再根据每一组数的乘积为1计算即可求出这m个数的积.
解答:解:(1)第17、18、19个数,分别为
,
,
;
(2)数
的前一个数为
,
的后一个数为
;
(3)m=1+2+3+…+2001+2=
+2=2003001+2=2003003,
这m个数的积=
×(
×
)×(
×
×
)×(
×
×
×
)×(
×
×
×
×
)×…×
×
=2003001.
故答案为:(1)
,
,
;(2)
,
.
| 2 |
| 5 |
| 3 |
| 4 |
| 4 |
| 3 |
(2)数
| 2 |
| a |
| 1 |
| a+1 |
| 2 |
| a |
| 3 |
| a-1 |
(3)m=1+2+3+…+2001+2=
| 2001×(2001+1) |
| 2 |
这m个数的积=
| 1 |
| 1 |
| 1 |
| 2 |
| 2 |
| 1 |
| 1 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
| 4 |
| 1 |
| 1 |
| 5 |
| 2 |
| 4 |
| 3 |
| 3 |
| 4 |
| 2 |
| 5 |
| 1 |
| 1 |
| 2002 |
| 2 |
| 2001 |
故答案为:(1)
| 2 |
| 5 |
| 3 |
| 4 |
| 4 |
| 3 |
| 1 |
| a+1 |
| 3 |
| a-1 |
点评:本题是对数字变化规律的考查,从分子的变化分子考虑求解是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图:已知正方形ABCD的边长为2cm,现在两动点P、Q分别从顶点B、A同时出发,当P沿线段BA以1cm/s的速度向点A运动,点Q沿折线A→D→C 以2cm/s的速度向C运动.设点P、Q运动的时间为t(秒)
如图:已知正方形ABCD的边长为2cm,现在两动点P、Q分别从顶点B、A同时出发,当P沿线段BA以1cm/s的速度向点A运动,点Q沿折线A→D→C 以2cm/s的速度向C运动.设点P、Q运动的时间为t(秒)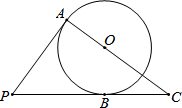 如图,PA、PB是⊙O的切线,切点分别为A、B,AO、PB的延长线相交于点C,⊙O的半径为3,BC=4,求切线PA的长.
如图,PA、PB是⊙O的切线,切点分别为A、B,AO、PB的延长线相交于点C,⊙O的半径为3,BC=4,求切线PA的长.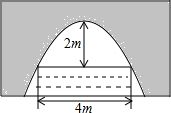 有一座抛物线形拱桥,正常水位时桥下水面宽度为4m,拱顶距离水面 2m.
有一座抛物线形拱桥,正常水位时桥下水面宽度为4m,拱顶距离水面 2m. 如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下四个结论:①AD=BE;②PQ∥AE;③AP=BQ;④△PCQ是等边三角形.恒成立的结论有( )
如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下四个结论:①AD=BE;②PQ∥AE;③AP=BQ;④△PCQ是等边三角形.恒成立的结论有( ) 如图所示,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2cm的速度向左运动,最终点A与点M重合.
如图所示,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2cm的速度向左运动,最终点A与点M重合. 如图,A、B为抛物线y=x2上的两点,且AB∥x轴,与y轴交于点C,以点O为圆心,OC为半径画圆,若AB=2
如图,A、B为抛物线y=x2上的两点,且AB∥x轴,与y轴交于点C,以点O为圆心,OC为半径画圆,若AB=2