题目内容
当k= 时,x2-kxy与y2+3xy-5的和中不含xy项.
考点:整式的加减
专题:
分析:先把x2-kxy+y2+3xy-5进行合并,然后令xy的系数为0即可得到k的值.
解答:解:x2-kxy+y2+3xy-5=x2+y2+(3-k)xy-5,
∵x2-kxy与y2+3xy-5的和中不含xy项,
∴3-k=0,
∴k=3.
故答案为3.
∵x2-kxy与y2+3xy-5的和中不含xy项,
∴3-k=0,
∴k=3.
故答案为3.
点评:本题考查了整式的加减:几个整式相加减,通常用括号把每一个整式括起来,再用加减号连接;然后去括号、合并同类项.整式的加减实质上就是合并同类项.

练习册系列答案
相关题目
 如图:已知正方形ABCD的边长为2cm,现在两动点P、Q分别从顶点B、A同时出发,当P沿线段BA以1cm/s的速度向点A运动,点Q沿折线A→D→C 以2cm/s的速度向C运动.设点P、Q运动的时间为t(秒)
如图:已知正方形ABCD的边长为2cm,现在两动点P、Q分别从顶点B、A同时出发,当P沿线段BA以1cm/s的速度向点A运动,点Q沿折线A→D→C 以2cm/s的速度向C运动.设点P、Q运动的时间为t(秒)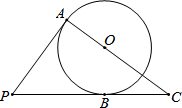 如图,PA、PB是⊙O的切线,切点分别为A、B,AO、PB的延长线相交于点C,⊙O的半径为3,BC=4,求切线PA的长.
如图,PA、PB是⊙O的切线,切点分别为A、B,AO、PB的延长线相交于点C,⊙O的半径为3,BC=4,求切线PA的长. 如图,A、B为抛物线y=x2上的两点,且AB∥x轴,与y轴交于点C,以点O为圆心,OC为半径画圆,若AB=2
如图,A、B为抛物线y=x2上的两点,且AB∥x轴,与y轴交于点C,以点O为圆心,OC为半径画圆,若AB=2