题目内容
观察下列等式:
13+23=
×4×9=
×22×33
13+23+33=36=
×9×16=
×32×42
13+23+33+43=100=
×14×25=
×42×52…
若n为正整数,试猜想13+23+33+4+…+n3等于多少?并利用此式比较13+23+33+4+…+1003与(-5000)2的大小.
13+23=
| 1 |
| 4 |
| 1 |
| 4 |
13+23+33=36=
| 1 |
| 4 |
| 1 |
| 4 |
13+23+33+43=100=
| 1 |
| 4 |
| 1 |
| 4 |
若n为正整数,试猜想13+23+33+4+…+n3等于多少?并利用此式比较13+23+33+4+…+1003与(-5000)2的大小.
考点:规律型:数字的变化类,有理数大小比较
专题:
分析:由所给的数据,得出变化规律,即是
乘以最后一个数的平方,再乘以最后一个数加1的平方,即可得出答案;根据所得出的规律,算出13+23+33+…+1003的结果,再与50002进行比较,即可得出答案.
| 1 |
| 4 |
解答:解:13+23+33+4+…+n3=
n2(n+1)2;
根据规律可知13+23+33+…+1003=
×1002×1012=5000×
>5000×5000.
因此13+23+33+…+1003>(-5000)2.
| 1 |
| 4 |
根据规律可知13+23+33+…+1003=
| 1 |
| 4 |
| 101×101 |
| 2 |
因此13+23+33+…+1003>(-5000)2.
点评:此题考查了数字的变化规律,通过观察、分析、总结得出题中的变化规律是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
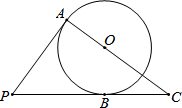 如图,PA、PB是⊙O的切线,切点分别为A、B,AO、PB的延长线相交于点C,⊙O的半径为3,BC=4,求切线PA的长.
如图,PA、PB是⊙O的切线,切点分别为A、B,AO、PB的延长线相交于点C,⊙O的半径为3,BC=4,求切线PA的长. 如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下四个结论:①AD=BE;②PQ∥AE;③AP=BQ;④△PCQ是等边三角形.恒成立的结论有( )
如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下四个结论:①AD=BE;②PQ∥AE;③AP=BQ;④△PCQ是等边三角形.恒成立的结论有( ) 如图所示,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2cm的速度向左运动,最终点A与点M重合.
如图所示,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2cm的速度向左运动,最终点A与点M重合. 如图,A、B为抛物线y=x2上的两点,且AB∥x轴,与y轴交于点C,以点O为圆心,OC为半径画圆,若AB=2
如图,A、B为抛物线y=x2上的两点,且AB∥x轴,与y轴交于点C,以点O为圆心,OC为半径画圆,若AB=2