题目内容
 如图,已知∠A=90°,∠B=15°,BD=DC,AC=4.求DB的长.
如图,已知∠A=90°,∠B=15°,BD=DC,AC=4.求DB的长.考点:含30度角的直角三角形
专题:
分析:根据等腰三角形性质求出∠DCB度数,根据三角形外角性质求出∠ADC,根据含30度角的直角三角形性质求出DC即可.
解答:解:∵∠B=15°,BD=DC,
∴∠DCB=∠B=15°,
∴∠ADC=∠B+∠BCD=30°,
∵在Rt△DAC中,∠A=90°,AC=4,∠ADC=30°,
∴DC=2AC=8,
∵DB=DC,
∴DB=8.
∴∠DCB=∠B=15°,
∴∠ADC=∠B+∠BCD=30°,
∵在Rt△DAC中,∠A=90°,AC=4,∠ADC=30°,
∴DC=2AC=8,
∵DB=DC,
∴DB=8.
点评:本题考查了等腰三角形性质,三角形外角性质,含30度角的直角三角形性质的应用,解此题的关键是求出DC=2AC,题目比较好,难度适中.

练习册系列答案
相关题目
 如图,EB=EC,EA=ED,AD=BC,∠AEB=∠DEC,证明:四边形ABCD是矩形.
如图,EB=EC,EA=ED,AD=BC,∠AEB=∠DEC,证明:四边形ABCD是矩形.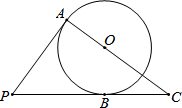 如图,PA、PB是⊙O的切线,切点分别为A、B,AO、PB的延长线相交于点C,⊙O的半径为3,BC=4,求切线PA的长.
如图,PA、PB是⊙O的切线,切点分别为A、B,AO、PB的延长线相交于点C,⊙O的半径为3,BC=4,求切线PA的长.