题目内容
1.如图,平行于x轴的直线AB与直线OB:y1=kx相交于点B,C为OB的中点,以C为顶点的抛物线y2=x2+bx+$\frac{1}{2}$经过点A、B,直线CD⊥x轴于点D.(1)求点A的坐标及b的值;
(2)将抛物线平移,得到的抛物线y3经过点A、D,与直线OB交于点E、F,当x为何值时,|y3-y1|的值随x的增大而减小?
(3)将抛物线再次作适当的平移,得抛物线y4=(x-h)2,若2<x≤m时,y4≤kx恒成立,求m的最大值.
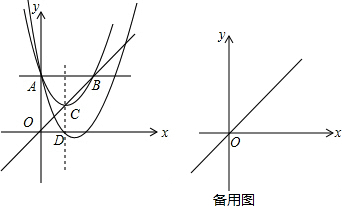
分析 (1)过点B作BE⊥x轴,垂足为E,将x=0代入抛物线的解析式可得到y=$\frac{1}{2}$,从而可求得点A的坐标,然后根据BE∥DC,可求得DC=$\frac{1}{4}$,然后利用二次函数的顶点坐标公式可求得b=±1,然后再根据对称轴的位置可知b=-1;
(2)将b=-1代入求得y2=x2-x+$\frac{1}{2}$,然后可求得点C的横坐标,从而得到点D的坐标为($\frac{1}{2}$,0),由点A和点D的坐标可求得y3=x2-$\frac{3}{2}x$+$\frac{1}{2}$,然后再求得y1=$\frac{1}{2}$x,然后可得到|y3-y1|=|x2-$\frac{3}{2}x$+$\frac{1}{2}$-$\frac{1}{2}x$|=|x2-2x+$\frac{1}{2}$|,然后根据x2-2x+$\frac{1}{2}$>0和x2-2x+$\frac{1}{2}$<0,化简绝对值,最后画出函数|y3-y1|=|x2-2x+$\frac{1}{2}$|的图象,根据函数图象可求得答案;
(3)将x=2代入y=$\frac{1}{2}x$得;y=1.将x=2,y=1代入y4=(x-h)2求得解得h=3,然后将y4=(x-3)2与y1=$\frac{1}{2}x$联立可求得:x1=2,x2=4.5,从而的求得m的最大值为4.5.
解答 解:(1)过点B作BE⊥x轴,垂足为E.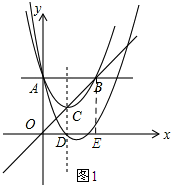
∵将x=0代入抛物线的解析式得y=$\frac{1}{2}$,
∴点A的坐标为(0,$\frac{1}{2}$).
∵AB∥x轴,
∴BE=OA=$\frac{1}{2}$.
∵BE∥DC,C是OB的中点,
∴△ODC∽△OEB.
∴$\frac{DC}{BE}=\frac{OC}{OB}=\frac{1}{2}$,即$\frac{DC}{\frac{1}{2}}=\frac{1}{2}$.
解得:DC=$\frac{1}{4}$.
由二次函数的顶点坐标公式可知:$\frac{4ac-{b}^{2}}{4a}$=$\frac{1}{4}$,即$\frac{{b}^{2}-4×1×\frac{1}{2}}{4×1}$=$\frac{1}{4}$.
解得:b=±1,
又∵x=-$\frac{b}{2a}$>0,
∴b=-1.
(2)∵b=-1,
∴y2=x2-x+$\frac{1}{2}$.
∴x=$-\frac{-1}{2×1}$=$\frac{1}{2}$.
∴点D的坐标为($\frac{1}{2}$,0).
设y3=x2+b1x+c1,将点A、点D的坐标代入函数的解析式得:$\left\{\begin{array}{l}{{c}_{1}=\frac{1}{2}}\\{\frac{1}{4}+\frac{1}{2}{b}_{1}+{c}_{1}=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{c}_{1}=\frac{1}{2}}\\{{b}_{1}=-\frac{3}{2}}\end{array}\right.$.
∴y3=x2-$\frac{3}{2}x$+$\frac{1}{2}$.
将点C的坐标代入y1=kx得:$\frac{1}{2}k=\frac{1}{4}$,解得;k=$\frac{1}{2}$.
∴y1=$\frac{1}{2}$x.
|y3-y1|=|x2-$\frac{3}{2}x$+$\frac{1}{2}$-$\frac{1}{2}x$|=|x2-2x+$\frac{1}{2}$|.
函数|y3-y1|=|x2-2x+$\frac{1}{2}$|的图象图2所示;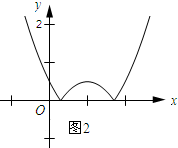
令x2-2x+$\frac{1}{2}$=0,解得:x1=1$+\frac{\sqrt{2}}{2}$,x2=1-$\frac{\sqrt{2}}{2}$.
x=-$\frac{b}{2a}$=$-\frac{-2}{1×2}$=1.
由函数图象可知:当x<1-$\frac{\sqrt{2}}{2}$或1<x$<1+\frac{\sqrt{2}}{2}$时,|y3-y1|的值随x的增大而减小.
(3)将x=2代入y=$\frac{1}{2}x$得;y=1.
将x=2,y=1代入y4=(x-h)2得:(2-h)2=1.
解得h=3或h=1(不合题意).
∴y4=(x-3)2.
根据题意得:(x-3)2=$\frac{1}{2}x$.
解得:x1=2,x2=4.5.
∴m的最大值为4.5.
点评 本题主要考查的是二次函数的综合应用、相似三角形的性质和判定、待定系数法求一次函数、二次函数的解析式、解一元二次方程,利用二次函数的图象和性质画出函数的图象是解题的关键.

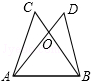 如图,AD=BC,AC=BD,则下列结论中,不正确的是( )
如图,AD=BC,AC=BD,则下列结论中,不正确的是( )| A. | OA=OB | B. | OC=OD | C. | ∠C=∠D | D. | ∠OAB=∠DBA |
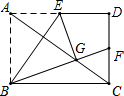 如图,在矩形ABCD中,点E为AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形ABCD的对角线AC上,延长BG交CD于F,连接EF.求$\frac{BE}{EF}$的值.
如图,在矩形ABCD中,点E为AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形ABCD的对角线AC上,延长BG交CD于F,连接EF.求$\frac{BE}{EF}$的值.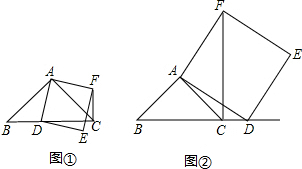
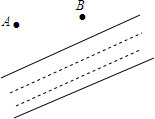 如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村和B村供水.
如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村和B村供水.