题目内容
17.骑车以25m/s的速度匀速行驶,司机突然发现前方有紧急情况,经过0.5s(从发现情况到开始制动刹车,司机的反应时间)开始制动刹车,又经过4.5s滑行60m车停止,则从发现情况到完全停止的这段时间内,汽车的平均速度为14.5m/s,如果这辆汽车从A地到B地的过程中,前半段路程的平均速度是20m/s,后半段路程的平均速度是30m/s,全程的平均速度为24m/s.分析 知道汽车的速度和反应时间,求出反应距离,求出反应距离和制动距离的总和,知道反应时间和制动时间,求出总时间,最后设汽车的平均速度为xm/s,根据速度公式求出汽车的平均速度;
设总路程为S米,分别求出前半段路程的时间,后半段路程的时间,再根据速度公式求出全程的平均速度.
解答 解:25×0.5=12.5(m),
12.5+60=72.5(m),
设汽车的平均速度为xm/s,
(0.5+4.5)x=72.5,
解得x=14.5.
设总路程为S米,则
$\frac{S}{\frac{\frac{1}{2}S}{20}+\frac{\frac{1}{2}S}{30}}$=$\frac{1}{\frac{\frac{3}{2}+\frac{2}{2}}{60}}$=24(m/s).
答:汽车的平均速度为14.5m/s,全程的平均速度为24m/s.
故答案为:14.5;24.
点评 考查了一元一次方程的应用,求全程的平均速度,一定想法求出全程的路程和全程的时间,然后根据速度公式求出汽车的平均速度.

练习册系列答案
相关题目
12.如果式子m-7与4m-9互为相反数,则m的值为( )
| A. | $\frac{16}{3}$ | B. | -$\frac{16}{3}$ | C. | $\frac{16}{5}$ | D. | -$\frac{16}{5}$ |
5.某商店以一定的价格购进某种干果若干千克,对其进行筛选分成甲级干果与乙级干果后同时开始销售.这批干果销售结束后,店主从销售统计中发出:甲级干果与乙级干果在销售过程中每天都有销量,于不同时间销售完;甲级干果从开始销售至销售的第x天的总销量y1(千克)与x的关系为y1=-x2+40x;乙级干果从开始销售至销售的第x天的总销量y2(千克)与x的关系为是二次函数,且乙级干果的前三天的销售量的情况见表:
(1)求乙级干果滴x天的总销量y2(千克)与x的函数关系式(不需要写自变量的取值范围);
(2)求:当一种干果销售完多长时间后,另一种干果才销售完?
(3)销售第几天时,两种干果的总销量相差最大?
| x | 1 | 2 | 3 |
| y2 | 58 | 112 | 162 |
(2)求:当一种干果销售完多长时间后,另一种干果才销售完?
(3)销售第几天时,两种干果的总销量相差最大?
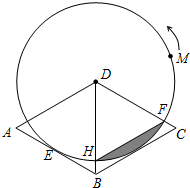 如图,在菱形ABCD中,∠A=60°,以点D为圆心的⊙D与边AB相切于点E.
如图,在菱形ABCD中,∠A=60°,以点D为圆心的⊙D与边AB相切于点E.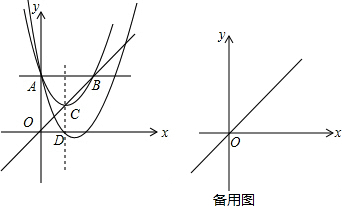
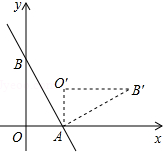 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,求点B′的坐标.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,求点B′的坐标.