题目内容
10.某检修小组乘汽车沿公路检修线路,约定前进为正,后退为负,某天自O地出发到收工时所走路线(单位:千米)为:+10、-3、+4、+2、-8、+13、-2、-12、+8、+5(1)问收工时距O地多远?
(2)若每千米耗油0.2升,从O地出发到收工时共耗油多少升?
分析 (1)约定前进为正,后退为负,依题意列式求出和即可;
(2)要求耗油量,需求他共走了多少路程,这与方向无关.
解答 解:(1)10-3+4+2-8+13-2-12+8+5=17(千米).
答:收工时距O地17千米;
(2)|+10|+|-3|+|+4|+|+2|+|-8|+|+13|+|-2|+|-12|+|+8|+|+5|=67,
67×0.2=13.4(升).
答:从O地出发到收工时共耗油13.4升.
点评 此题主要考查了正数与负数,正确理解正负数的意义是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.若x与4-4x的值互为相反数,则x的值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{1}{2}$ |
5.某商店以一定的价格购进某种干果若干千克,对其进行筛选分成甲级干果与乙级干果后同时开始销售.这批干果销售结束后,店主从销售统计中发出:甲级干果与乙级干果在销售过程中每天都有销量,于不同时间销售完;甲级干果从开始销售至销售的第x天的总销量y1(千克)与x的关系为y1=-x2+40x;乙级干果从开始销售至销售的第x天的总销量y2(千克)与x的关系为是二次函数,且乙级干果的前三天的销售量的情况见表:
(1)求乙级干果滴x天的总销量y2(千克)与x的函数关系式(不需要写自变量的取值范围);
(2)求:当一种干果销售完多长时间后,另一种干果才销售完?
(3)销售第几天时,两种干果的总销量相差最大?
| x | 1 | 2 | 3 |
| y2 | 58 | 112 | 162 |
(2)求:当一种干果销售完多长时间后,另一种干果才销售完?
(3)销售第几天时,两种干果的总销量相差最大?
19.某电器厂生产一种新产品,在定价时不单是根据生产成本而定,还要请各消费单位来出价,即他们愿意以什么价格来购买.根据调查得出需求函数x=-900P+45000,该厂生产该产品的固定成本是270000元,而单位产品的变动成本为10元,为获得最大利润,出厂价格应为( )
| A. | 9000(单位) | B. | 8000(单位) | C. | 1000(单位) | D. | 18000(单位) |
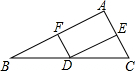 如图,点D是BC的中点,DE垂直平分AC,垂足为E,F是BA的中点,求证:DF是AB的垂直平分线.
如图,点D是BC的中点,DE垂直平分AC,垂足为E,F是BA的中点,求证:DF是AB的垂直平分线. 某商场老板对一种新上市商品的销售情况进行记录,已知这种商品进价为每件40元,经过记录分析发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
某商场老板对一种新上市商品的销售情况进行记录,已知这种商品进价为每件40元,经过记录分析发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示. 已知y=$\frac{1}{2}$x2+2x+1
已知y=$\frac{1}{2}$x2+2x+1