题目内容
13.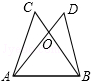 如图,AD=BC,AC=BD,则下列结论中,不正确的是( )
如图,AD=BC,AC=BD,则下列结论中,不正确的是( )| A. | OA=OB | B. | OC=OD | C. | ∠C=∠D | D. | ∠OAB=∠DBA |
分析 根据全等三角形的性质得到∠C=∠D,∠ABC=∠BAD,AD=BC,由等腰三角形的性质得到OA=OB,于是得到OC=OD,由于∠DBA>∠CBA,得到∠DBA>∠OAB,即可得到结论.
解答 证明:在△ABC与△BAD中,
$\left\{\begin{array}{l}{AD=BC}\\{AC=BD}\\{AB=AB}\end{array}\right.$,
∴△ABC≌△ABD,
∴∠C=∠D,∠ABC=∠BAD,AD=BC,
∴OA=OB,
∴AD-AO=BC-BO,
即OC=OD,
∴A,B,C选项正确,
∵∠DBA>∠CBA,
∴∠DBA>∠OAB,
∴D选项错误,
故选D.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
5.某商店以一定的价格购进某种干果若干千克,对其进行筛选分成甲级干果与乙级干果后同时开始销售.这批干果销售结束后,店主从销售统计中发出:甲级干果与乙级干果在销售过程中每天都有销量,于不同时间销售完;甲级干果从开始销售至销售的第x天的总销量y1(千克)与x的关系为y1=-x2+40x;乙级干果从开始销售至销售的第x天的总销量y2(千克)与x的关系为是二次函数,且乙级干果的前三天的销售量的情况见表:
(1)求乙级干果滴x天的总销量y2(千克)与x的函数关系式(不需要写自变量的取值范围);
(2)求:当一种干果销售完多长时间后,另一种干果才销售完?
(3)销售第几天时,两种干果的总销量相差最大?
| x | 1 | 2 | 3 |
| y2 | 58 | 112 | 162 |
(2)求:当一种干果销售完多长时间后,另一种干果才销售完?
(3)销售第几天时,两种干果的总销量相差最大?
3.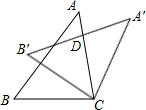 如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )
如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )
 如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )
如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )| A. | 48° | B. | 58° | C. | 68° | D. | 78° |
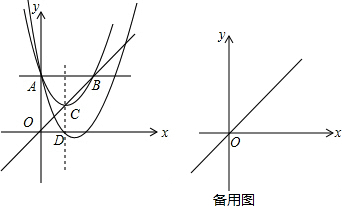
 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,求点B′的坐标.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,求点B′的坐标.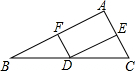 如图,点D是BC的中点,DE垂直平分AC,垂足为E,F是BA的中点,求证:DF是AB的垂直平分线.
如图,点D是BC的中点,DE垂直平分AC,垂足为E,F是BA的中点,求证:DF是AB的垂直平分线. 已知y=$\frac{1}{2}$x2+2x+1
已知y=$\frac{1}{2}$x2+2x+1