题目内容
19. 将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠EFB,则∠GFH等于( )
将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠EFB,则∠GFH等于( )| A. | 80° | B. | 85° | C. | 90° | D. | 95° |
分析 根据折叠求出∠CFG=∠EFG=$\frac{1}{2}$∠CFE,根据角平分线定义求出∠HFE=$\frac{1}{2}$∠BFE,即可求出∠GFH=∠GFE+∠HFE=$\frac{1}{2}$∠CFB.
解答 解:∵将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,
∴∠CFG=∠EFG=$\frac{1}{2}$∠CFE,
∵FH平分∠BFE,
∴∠HFE=$\frac{1}{2}$∠BFE,
∴∠GFH=∠GFE+∠HFE=$\frac{1}{2}$(∠CFE+∠BFE)=$\frac{1}{2}$×180°=90°,
即∠GFH是直角.
故选C.
点评 本题考查了角的计算,折叠的性质,角平分线定义的应用,综合运用定义是解答此题的关键.

练习册系列答案
相关题目
7.已知抛物线y=ax2+bx+c的对称轴是x=2,且经过点(1,0),则9a+3b+c的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 3 |
14.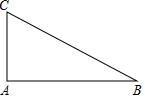 如图,在Rt△ABC中,已知∠A=90°,AC=3,AB=4,则sinB等于( )
如图,在Rt△ABC中,已知∠A=90°,AC=3,AB=4,则sinB等于( )
 如图,在Rt△ABC中,已知∠A=90°,AC=3,AB=4,则sinB等于( )
如图,在Rt△ABC中,已知∠A=90°,AC=3,AB=4,则sinB等于( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
9. 如图,能使AB∥CD的条件是( )
如图,能使AB∥CD的条件是( )
 如图,能使AB∥CD的条件是( )
如图,能使AB∥CD的条件是( )| A. | ∠1=∠B | B. | ∠3=∠A | C. | ∠BCD+∠B=180° | D. | ∠1=∠A |