题目内容
14.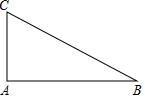 如图,在Rt△ABC中,已知∠A=90°,AC=3,AB=4,则sinB等于( )
如图,在Rt△ABC中,已知∠A=90°,AC=3,AB=4,则sinB等于( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
分析 利用勾股定理列式求出BC,再根据锐角的正弦等于对边比斜边列式即可.
解答 解:由勾股定理得,BC=$\sqrt{A{C}^{2}+A{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
所以,sinB=$\frac{AC}{BC}$=$\frac{3}{5}$.
故选B.
点评 本题考查了锐角三角函数的定义,勾股定理,主要利用了锐角的正弦等于对边比斜边.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
2.已知a,b,c,d是成比例线段,其中a=3cm,b=2cm,c=6cm,则d的长度为( )
| A. | 4cm | B. | 5cm | C. | 6cm | D. | 9cm |
19. 将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠EFB,则∠GFH等于( )
将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠EFB,则∠GFH等于( )
 将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠EFB,则∠GFH等于( )
将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠EFB,则∠GFH等于( )| A. | 80° | B. | 85° | C. | 90° | D. | 95° |
6.下列命题的逆命题为假命题的是( )
| A. | 若a=0,则ab=0 | |
| B. | 内错角相等,两直线平行 | |
| C. | 若两个角相等,那么这两个角都为30° | |
| D. | 若|a|=|b|,则a=b |
4.用配方法解方程x2+4x+1=0,配方后的方程是( )
| A. | (x+2)2=5 | B. | (x-2)2=3 | C. | (x-2)2=5 | D. | (x+2)2=3 |
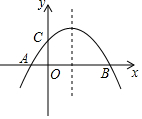 如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.
如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.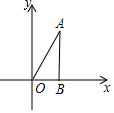 如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O旋转150°得到△OA′B′,则点A′的坐标为(0,-4)或(-2$\sqrt{3}$,-2).
如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O旋转150°得到△OA′B′,则点A′的坐标为(0,-4)或(-2$\sqrt{3}$,-2).