题目内容
7.某数学活动小组在做角的拓展图形练习时,经历了如下过程:(1)操作发现:
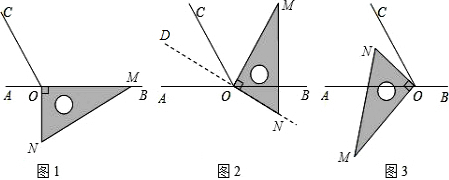
点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方,如图1.将图1中的三角板绕点O旋转,当直角三角板的OM边在∠BOC的内部,且恰好平分∠BOC时,如图2.
则下列结论正确的是①②④(填序号即可)
①∠BOM=60°;②∠COM-∠BON=30°;③OB平分∠MON;④∠AOC的平分线在直线ON上.
(2)数学思考:
同学们在操作中发现,当三角板绕点O旋转时,如果直角三角板的OM边在∠BOC的内部且另一边ON在直线AB的下方,那么∠COM与∠BON的差不变,请你说明理由;如果直角三角板的OM、ON边都在∠BOC的内部,那么∠COM与∠BON的和不变,请直接写出∠COM与∠BON的和,不要求说明理由.
(3)类比探索:
三角板绕点O继续旋转,当直角三角板的ON边在∠AOC的内部时,如图3.求∠AOM与∠CON相差多少度?为什么?
分析 (1)利用角平分线的定义结合直角三角板的内角度数即可分别判断得出答案;
(2)首先根据∠COM=120°-∠BOM,∠BON=90°-∠BOM,进而得出答案;
(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°-∠AON,∠NOC=60°-∠AON,然后作差即可.
解答 解:(1)∵∠BOC=120°,OM平分∠BOC,
∴∠BOM=60°,故①正确;
∵∠BOM=60°,∠MON=90°,
∴∠COM=60°,∠BON=30°,
∴∠COM-∠BON=30°,故②正确;
∵∠BOM=60°,∠BON=30°,
∴OB平分∠MON,错误;
∵∠BOC=120°,∠BON=30°,
∴∠AOD=∠COD=30°,
∴∠AOC的平分线在直线ON上,故④正确;
故答案为:①②④;
(2)①∵∠COM=120°-∠BOM,
∠BON=90°-∠BOM,
∴∠COM-∠BON=120°-90°=30°;
②由题意可得:∠COM+∠BON=120°-90°=30°;
(3)∵∠AOM=90°-∠AON,∠CON=∠AOC-∠AON=60°-∠AON,
∴∠AOM-∠CON=90°-60°=30°.
点评 此题考查了角平分线的定义,应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
19.下列各式正确的是( )
| A. | -(+8)=8 | B. | -(-3)=-3 | C. | -$\frac{2}{3}$<-$\frac{1}{2}$ | D. | -π>-3.14 |
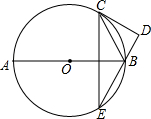 如图,AB为⊙O的直径,C为⊙O上一点,CD切⊙O于点C,BD⊥CD,BD交⊙O于点E,连CE.
如图,AB为⊙O的直径,C为⊙O上一点,CD切⊙O于点C,BD⊥CD,BD交⊙O于点E,连CE.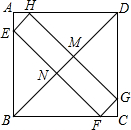 如图,四边形EFGH的四个顶点E、F、G、H分别在正方形ABCD的AB、BC、CD、DA上滑动,在滑动的过程中,始终有EH∥BD∥FG,且EH=FG,四边形EFGH的周长为$2\sqrt{2}a$,那么正方形ABCD的周长为4a.
如图,四边形EFGH的四个顶点E、F、G、H分别在正方形ABCD的AB、BC、CD、DA上滑动,在滑动的过程中,始终有EH∥BD∥FG,且EH=FG,四边形EFGH的周长为$2\sqrt{2}a$,那么正方形ABCD的周长为4a.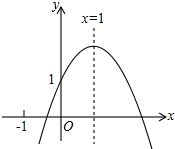 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①c<1;②2a+b=0;③已知点A(x1,y1),B(x2,y2)在该抛物线上,当x1>x2,则y1>y2;④若方程ax2+bx+c=0有两个根,其中一个根为3,则另一个根为-1,则正确的结论是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①c<1;②2a+b=0;③已知点A(x1,y1),B(x2,y2)在该抛物线上,当x1>x2,则y1>y2;④若方程ax2+bx+c=0有两个根,其中一个根为3,则另一个根为-1,则正确的结论是( )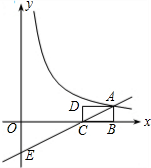 如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E,反比例函数y=$\frac{m}{x}$的图象经过点A.
如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E,反比例函数y=$\frac{m}{x}$的图象经过点A. 某校为了解学生喜爱的体育活动项目,随机抽查了100名学生,让每人选一项自己喜欢的项目,并制成如图所示的扇形统计图.如果该校有600名学生,则喜爱跳绳的学生约有180人.
某校为了解学生喜爱的体育活动项目,随机抽查了100名学生,让每人选一项自己喜欢的项目,并制成如图所示的扇形统计图.如果该校有600名学生,则喜爱跳绳的学生约有180人.