题目内容
18.若式子(x+1)0+$\sqrt{x+2}$+(x-2)-2有意义,则x的取值范围为-2≤x<-1且-1<x<2,x>2.分析 根据非零的零次幂等于,被开方数是非负数,负整数指数幂与正整数指数幂互为倒数,可得关于x的不等式组,根据解不等式组,可得答案.
解答 解:由(x+1)0+$\sqrt{x+2}$+(x-2)-2有意义,得
$\left\{\begin{array}{l}{x+1≠0}\\{x+2≥0}\\{x-2≠0}\end{array}\right.$.
解得-2≤x<-1且-1<x<2,x>2.
故答案为:-2≤x<-1且-1<x<2,x>2.
点评 本题考查了负整数指数幂,利用非零的零次幂等于,被开方数是非负数,负整数指数幂与正整数指数幂互为倒数得出关于x的不等式组是解题关键.

练习册系列答案
相关题目
4. 请解答问题:
请解答问题:
(1)某种细胞分裂时由1个分裂成2个,2个分裂成4个,…一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x之间构成一个函数关系,请写出y与x之间的关系可以表示为y=2x;
(2)将此问题一般化,在定义域为全体实数时,试列表研究此函数的图象与性质:
(3)观察图象,请写出你认为正确的结论:①函数的图象是抛物线②函数的图象在一、二象限,y随x的增大而增大③函数图象经过(0,1)点,且与x轴没有交点.
 请解答问题:
请解答问题:(1)某种细胞分裂时由1个分裂成2个,2个分裂成4个,…一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x之间构成一个函数关系,请写出y与x之间的关系可以表示为y=2x;
(2)将此问题一般化,在定义域为全体实数时,试列表研究此函数的图象与性质:
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y |
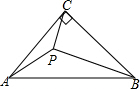 如图,在△ABC中,∠ACB=90°,AC=BC,P为三角形内部一点,且PC=3,PA=5,PB=7,则△PAB的面积为14.
如图,在△ABC中,∠ACB=90°,AC=BC,P为三角形内部一点,且PC=3,PA=5,PB=7,则△PAB的面积为14.