题目内容
5.下列根式:$\sqrt{4{a^2}+13},\sqrt{18x+9},-2\sqrt{4x},\sqrt{\frac{2}{3}},\frac{{\sqrt{2}}}{3},\sqrt{11{x^3}},\frac{1}{{\sqrt{2}}}$中,最简二次根式共有2个.分析 根据最简二次根式的概念进行判断即可.
解答 解:$\sqrt{4{a}^{2}+13}$、$\frac{\sqrt{2}}{3}$是最简二次根式,
$\sqrt{18x+9}$=3$\sqrt{2x+1}$,-2$\sqrt{4x}$=-4$\sqrt{x}$,$\sqrt{11{x}^{3}}$=x$\sqrt{11x}$,不是最简二次根式,
$\sqrt{\frac{2}{3}}$和$\frac{1}{\sqrt{2}}$被开方数含有分母,不是最简二次根式,
故答案为:2.
点评 本题考查的是最简二次根式的概念,最简二次根式的概念:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.

练习册系列答案
相关题目
15.已知?ABCD的两条对角线AC=18,BD=8,则BC的长度可能为( )
| A. | 5 | B. | 10 | C. | 13 | D. | 26 |
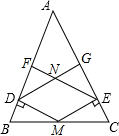 已知:如图,M是等腰三角形ABC的底边BC的中点,MD⊥AB,ME⊥AC,EF⊥AB,DG⊥AC,垂足分别为为D,E,F,G,DG与EF交于点N,求证:四边形DMEN是菱形.
已知:如图,M是等腰三角形ABC的底边BC的中点,MD⊥AB,ME⊥AC,EF⊥AB,DG⊥AC,垂足分别为为D,E,F,G,DG与EF交于点N,求证:四边形DMEN是菱形. 如图,在?ABCD中,AE⊥BC,AF⊥CD,∠EAF=60°,BE=2,DF=3.求:
如图,在?ABCD中,AE⊥BC,AF⊥CD,∠EAF=60°,BE=2,DF=3.求: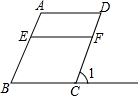 如图,E在AB上,F在DC上,G是BC延长线上的一点:
如图,E在AB上,F在DC上,G是BC延长线上的一点: