题目内容
 如图,在Rt△ABC中,∠C=90°,顶点A、C的坐标分别为(-1,2),(3,2),点B在x轴上,抛物线y=-x2+bx+c经过A、C两点.
如图,在Rt△ABC中,∠C=90°,顶点A、C的坐标分别为(-1,2),(3,2),点B在x轴上,抛物线y=-x2+bx+c经过A、C两点.(1)求该抛物线所对应的函数关系式;
(2)点P是抛物线上的一点,当S△PAB=
| 5 |
| 4 |
(3)若点N由点B出发,以每秒
| 6 |
| 5 |
| 1 |
| 3 |
考点:二次函数综合题
专题:
分析:(1)根据抛物线y=-x2+bx+c经过A、C两点,把(-1,2),(3,2)代入y=-x2+bx+c计算即可;
(2)先求出 yAB=-
x+
,再求出
S△ABC=5,分两种情况讨论:
当P在AB上方时,根据S△PAB=S△PAQ+S△PBQ=2PQ得出2[(-x2+2x+5)-(-
x+
)]=5;
当P在AB下方时,根据S△PAB=S△PQB-S△PQA=2PQ得出2[(-
x+
)-(-x2+2x+5)]=5,再分别求解即可;
(3)当点N在BC上时,设MN与AB交于点D,若MN⊥AB,根据△BMN∽△CBA,得出
=
,再根据BN=
5t,BM=t-
,得出
=
,当点N在CA上时,设MN与AB交于点D,过点N作NE⊥x轴于点E,则CN=EB,根据△ACB∽△NEM,得出
=
,求出EM=1,再求出EB=t-
,再根据CN=
t-2,得出
t-2=t-
,再分别求出t即可.
(2)先求出 yAB=-
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
当P在AB上方时,根据S△PAB=S△PAQ+S△PBQ=2PQ得出2[(-x2+2x+5)-(-
| 1 |
| 2 |
| 3 |
| 2 |
当P在AB下方时,根据S△PAB=S△PQB-S△PQA=2PQ得出2[(-
| 1 |
| 2 |
| 3 |
| 2 |
(3)当点N在BC上时,设MN与AB交于点D,若MN⊥AB,根据△BMN∽△CBA,得出
| BN |
| CA |
| BM |
| BC |
| 6 |
| 5 |
| 1 |
| 3 |
| ||
| 4 |
t-
| ||
| 2 |
| AC |
| NE |
| CB |
| EM |
| 4 |
| 3 |
| 6 |
| 5 |
| 6 |
| 5 |
| 4 |
| 3 |
解答:解:(1)∵抛物线y=-x2+bx+c经过A、C两点,
∴把(-1,2),(3,2)代入得:
,
解得:
,
∴该抛物线所对应的函数关系式为:y=-x2+2x+5;
(2)由A(-1,2)B(3,0)可得:yAB=-
x+
,
∵S△ABC=
AC•BC=
×4×2=4,
∴
S△ABC=
×4=5,
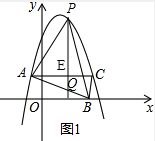 如图1,当P在AB上方时,
如图1,当P在AB上方时,
S△PAB=S△PAQ+S△PBQ=
PQ•AE+
PQ•CE=
PQ•AC=
•PQ×4=2PQ=2[(-x2+2x+5)-(-
x+
)]=5,
解得:x1=
,x2=
,
则P1(
,
)P2(
,
)
如图2,当P在AB下方时,
S△PAB=S△PQB-S△PQA=
PQ•BG-
PQ•GF=
PQ•AC=
•PQ×4=2PQ=2[(-
x+
)-(-x2+2x+5)]=5,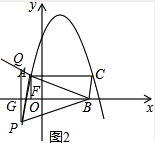
解得:x1=-
,x2=4,
则P3(-
,-
),P4(4,-3),
综上所述:P1(
,
),P2(
,
),P3(-
,-
),P4(4,-3);
(3)如图3,当点N在BC上时,设MN与AB交于点D,
若MN⊥AB,
∵∠BDN=∠BCA,∠B=∠B,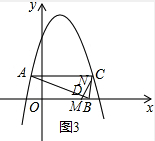
∴∠BND=∠BAC,
∵∠MBC=∠ACB=90°,
∴△BMN∽△CBA,
∴
=
,
∵BN=
5t,BM=t-
,
∴
=
,
∴t=
(秒),
如图4,当点N在CA上时,设MN与AB交于点D,
过点N作NE⊥x轴于点E,则CN=EB,
若MN⊥AB,则∠A=∠MNE,
∵∠ACB=∠MEN,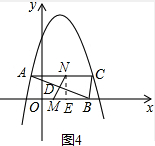
∴△ACB∽△NEM,
∴
=
,
∴
=
,
∴EM=1,
∴EB=MB-EM=t-
-1=t-
,
∵CN=
t-2,∴
t-2=t-
,
∴t=
.
∴把(-1,2),(3,2)代入得:
|
解得:
|
∴该抛物线所对应的函数关系式为:y=-x2+2x+5;
(2)由A(-1,2)B(3,0)可得:yAB=-
| 1 |
| 2 |
| 3 |
| 2 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 5 |
| 4 |
| 5 |
| 4 |
 如图1,当P在AB上方时,
如图1,当P在AB上方时,S△PAB=S△PAQ+S△PBQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解得:x1=
5+
| ||
| 4 |
5-
| ||
| 4 |
则P1(
5+
| ||
| 4 |
27-
| ||
| 8 |
5-
| ||
| 4 |
27+
| ||
| 8 |
如图2,当P在AB下方时,
S△PAB=S△PQB-S△PQA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |

解得:x1=-
| 3 |
| 2 |
则P3(-
| 3 |
| 2 |
| 1 |
| 4 |
综上所述:P1(
5+
| ||
| 4 |
27-
| ||
| 8 |
5-
| ||
| 4 |
27+
| ||
| 8 |
| 3 |
| 2 |
| 1 |
| 4 |
(3)如图3,当点N在BC上时,设MN与AB交于点D,
若MN⊥AB,
∵∠BDN=∠BCA,∠B=∠B,

∴∠BND=∠BAC,
∵∠MBC=∠ACB=90°,
∴△BMN∽△CBA,
∴
| BN |
| CA |
| BM |
| BC |
∵BN=
| 6 |
| 5 |
| 1 |
| 3 |
∴
| ||
| 4 |
t-
| ||
| 2 |
∴t=
| 5 |
| 6 |
如图4,当点N在CA上时,设MN与AB交于点D,
过点N作NE⊥x轴于点E,则CN=EB,
若MN⊥AB,则∠A=∠MNE,
∵∠ACB=∠MEN,

∴△ACB∽△NEM,
∴
| AC |
| NE |
| CB |
| EM |
∴
| 4 |
| 2 |
| 2 |
| EM |
∴EM=1,
∴EB=MB-EM=t-
| 1 |
| 3 |
| 4 |
| 3 |
∵CN=
| 6 |
| 5 |
| 6 |
| 5 |
| 4 |
| 3 |
∴t=
| 10 |
| 3 |
点评:此题考查了二次函数的综合,用到的知识点是待定系数法求函数的解析式、相似三角形的性质、三角形的面积、矩形的性质,关键是根据题意画出图形,注意分类讨论思想的运用,不要漏解.

练习册系列答案
相关题目
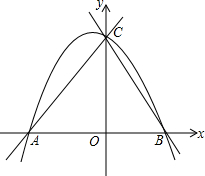 如图,二次函数y=ax2+2ax+4的图象与x轴交于点A、B,与y轴交于点C,OC:OB=2:1,
如图,二次函数y=ax2+2ax+4的图象与x轴交于点A、B,与y轴交于点C,OC:OB=2:1,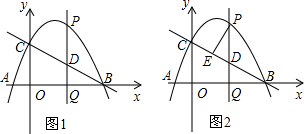
 已知抛物线y=-x2+2x+m-2与y轴交于点A(0,2m-7),与直线y=2x交于点B,C(B在C的右侧).求抛物线的解析式.
已知抛物线y=-x2+2x+m-2与y轴交于点A(0,2m-7),与直线y=2x交于点B,C(B在C的右侧).求抛物线的解析式.